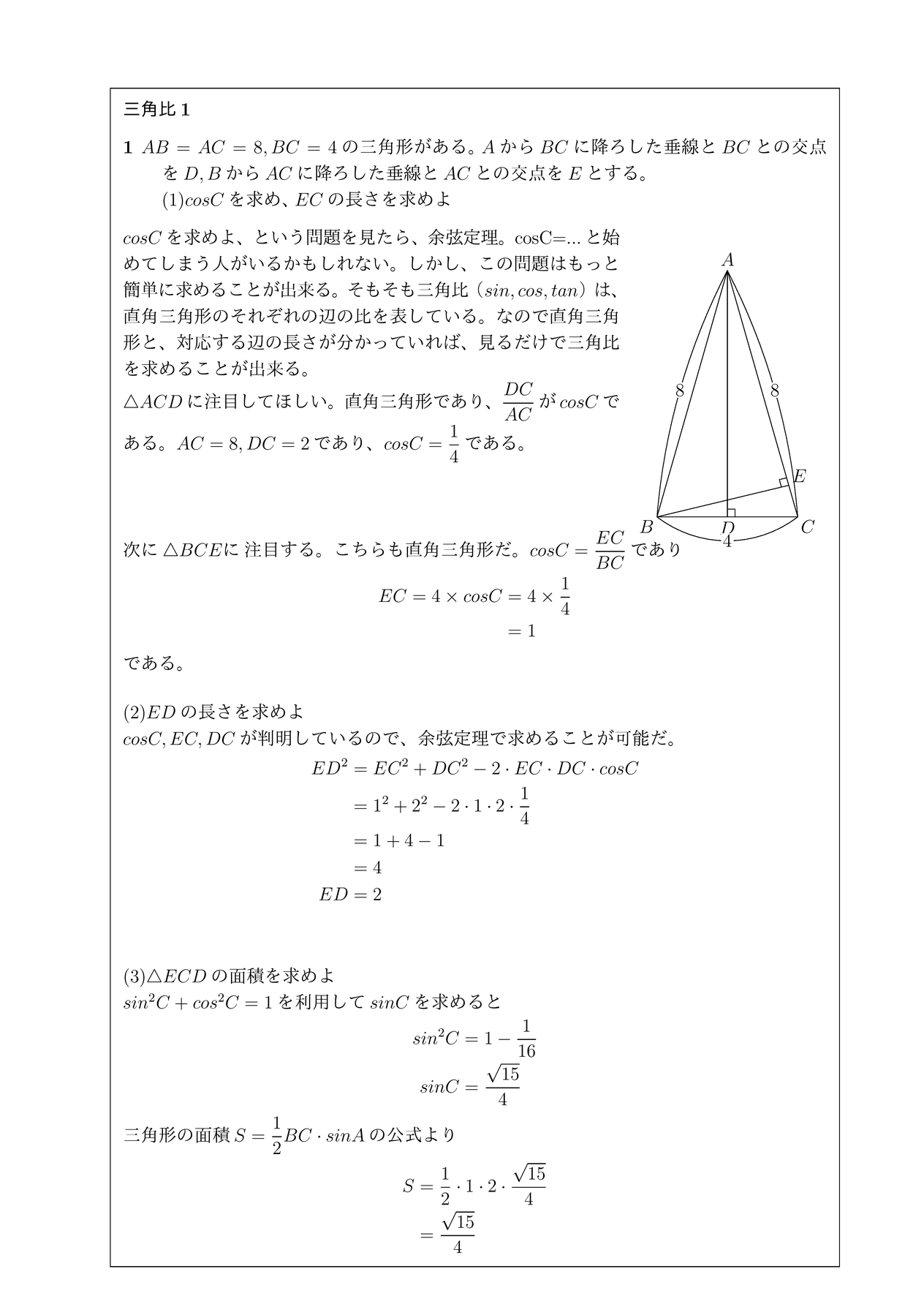
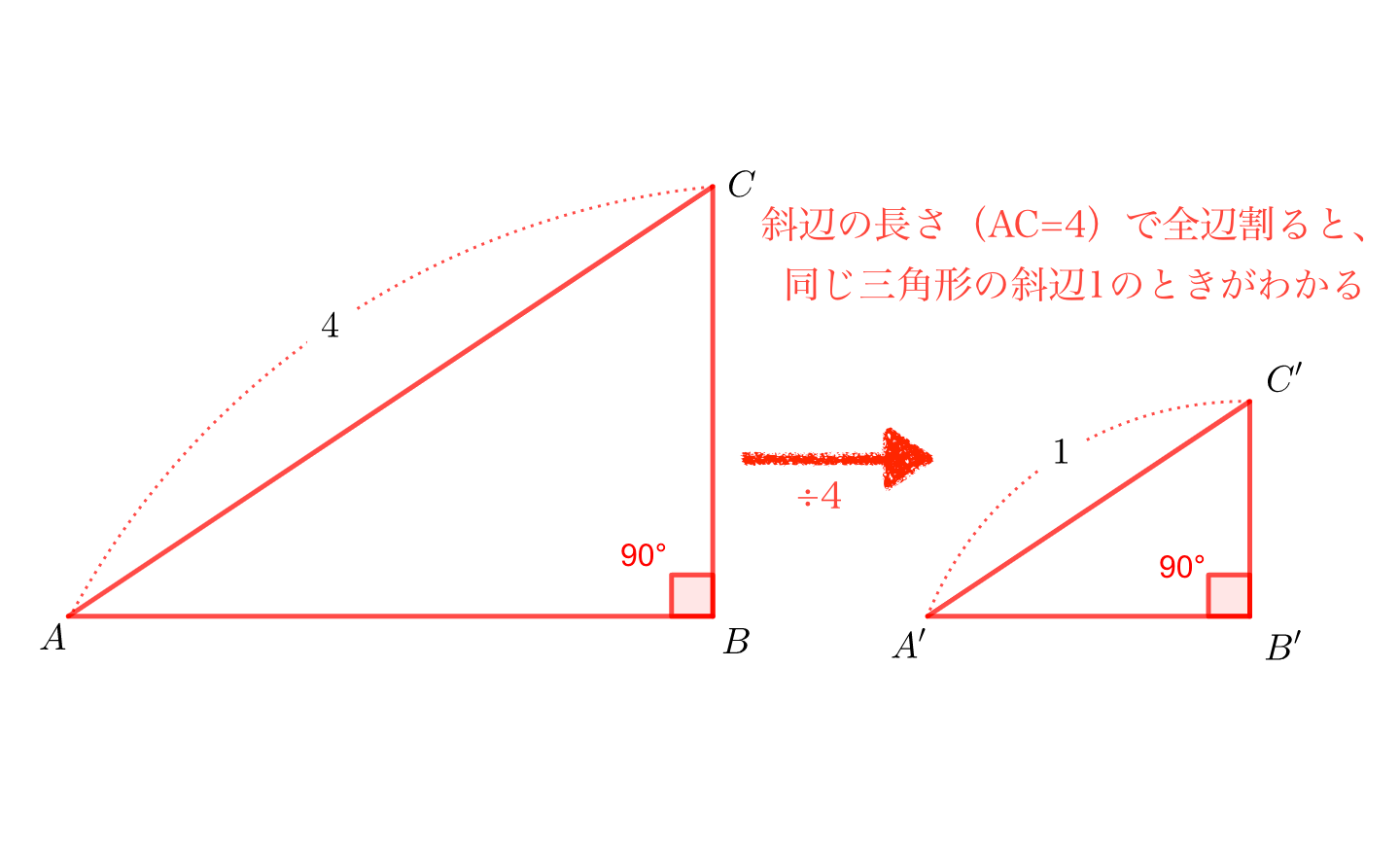
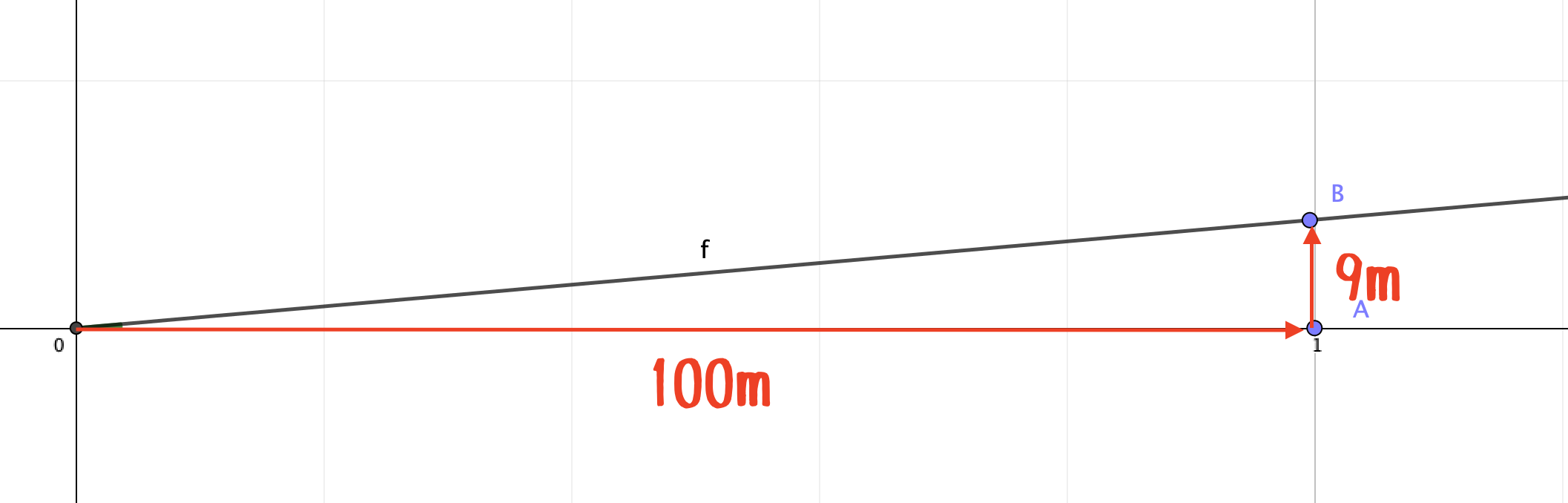
特定の2点間を線でつなぐのを Unity でどう書けばいいのか、いつもやりかたを忘れてしまうのでまとめておきます。 2点間の線の長さ 下記のような直角三角形があるとして、 = なので、 斜辺は、 = で求められます。 Unity で書くとこんな感じですかね。特定の2点間を線でつなぐのを Unity でどう書けばいいのか、いつもやりかたを忘れてしまうのでまとめておきます。 2点間の線の長さ 下記のような直角三角形があるとして、 = なので、 斜辺は、 = で求められます。 Unity で書くとこんな感じですかね。Pythonではnparctan2(高さ、底辺)を使うとradianが帰ってくるので、これをdegrees()で度数に変換します。 以下では$\sqrt{3}$と1で角度を求めます。 #角度を求める import numpy as np round ( np degrees ( np arctan2 ( np sqrt ( 3 ), 1 ))) #> 600

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
角度 求め 方 斜辺 高さ
角度 求め 方 斜辺 高さ-計算例 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 \) お客様の声 アンケート投稿 よくある質問 リンク方法 底辺と高さから角度と斜辺を計算 底辺と高さから角度と斜辺を計算 にリンクを張る方法三平方の定理の計算角度と長さ 三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求めることができる。 角度について 角度



Android용 底辺と高さから斜辺と角度計算 Apk 다운로드
・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数 ・角度から三角関数 角度(度またはラジアン)から三角関数を計算します。 ・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。特定の2点間を線でつなぐのを Unity でどう書けばいいのか、いつもやりかたを忘れてしまうのでまとめておきます。 2点間の線の長さ 下記のような直角三角形があるとして、 = なので、 斜辺は、 = で求められます。 Unity で書くとこんな感じですかね。数学・算数 底辺5cm、高さ3cm、角度Θの三角形があったとし、 tanΘの求め方が tanΘ=3/5=06となり、 角度Θ=atan(06)=30°となるというのはわかったのですが、 at
計算例 底辺と高さから角度と斜辺を計算 斜辺 c 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 \) お客様の声 アンケート投稿 よくある質問 リンク方法 底辺と高さから角度と斜辺を計算斜辺距離 2 勾配(%)、(度)の 相互変換 勾配(%) 勾配(度) 勾配(度) 勾配(%) 3 勾配から水平距離、 垂直距離の計算 勾配(%) または 勾配(度) 水平距離 または 垂直距離 水平距離 垂直距離 斜辺距離 計算式 1.水平距離・垂直距離Q 角度θと斜辺の長さから底辺と対辺の長さの求め方を・・ すみません、「計算式」を教えて頂きたいのですが、 角度θと斜辺の長さが解っている垂直三角形から 底辺と対辺の長さの数字を求めるにはどう計算すればよろしいのでしょうか?
さて、具体的に角Aの余弦、つまり\(\cos A\)を求めてみます。 公式の使い方ですが、実は頭の中では次のように考えて使います。 求めたい角度の対辺はどれか? 求めたい角度を挟んでいる辺はどれか? もし、求めたい角がAであるのなら、 対辺はa、計算例 底辺と高さから角度と斜辺を計算 斜辺 c 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 \) お客様の声 アンケート投稿 よくある質問 リンク方法 底辺と高さから角度と斜辺を計算新着三角形 角度 出し 方 三角形の辺の長さや角度の計算に便利 Standby 三角形の辺から角度を計算 製品設計知識 底辺と高さから角度と斜辺を計算 高精度計算サイト



三角関数 あ そんなことか


三角比を使った問題1 チーム エン
数学・算数 等脚台形の高さと角度 等脚台形の底辺aと上辺bの長さがわかる場合、高さと底辺の角度の求め方教えて下さい。 低レベルですいません。 質問No特に、直角三角形の一辺の長さと直角以外のいずれかの角の角度が分かれば、斜辺の長さが求められます。 辺 a 、 b 、 c と、角 A 、 B 、 C の三角形があるとすると、正弦定理は a / sin A = b / sin B = c / sin C であることを示しています。三平方の定理の計算角度と長さ 三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求めることができる。 角度について 角度



電験3種の基礎数学 三角比と三角関数 基礎からわかる電気技術者の知識と資格



やさしい寄せスラブの計算 池坊徳夫のブログ 型枠計算法
6.直角三角形の底辺と高さと角度の計算(TAN関数) 問題 直角三角形の高さ、底辺、鋭角の角度のうち2つが分かっていれば残り1つを求めることができる。空欄を求めなさい。 解説 底辺(横幅)の長さに対する、高さの比率をtan(タンジェント)といいエクセルで斜辺と高さから角度を求める方法 斜辺と高さから、三角形の角度θを計算することも同様の手順で行うことができます。 なお、斜辺と高さから直角三角形の角度を求めていくには、三角関数であるsin(サイン)の逆関数sin1を使用します。また、arctanで求めた結果はラジアンで出てくるので 角度(°) = arctan(勾配) × 360 ÷ π で計算することができる。 距離の計算 三平方の定理より 斜辺 2 = 水平距離 2 + 高さ 2 で求められる。 角度と勾配(%)の換算 角度と%の換算は 角度→勾配(%)



三角比 文章題 高校数学に関する質問 勉強質問サイト


三角関数の加法定理の導出 N S Note
この記事では、三角関数について、角度の求め方や変換公式 (\\(90^\\circ − \\theta\\) など) について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいねなるほど、平たく言うと角度の単位のことか。。 角度をラジアンに変換する これは、 rad = θ * (π / 180) で求まるようです。 ちなみに、2π = 360° ちなみに、1π = 180°です 三角形の面積の求め方 まとめ 三角形の面積をJavaで求めるには直角三角形(例) 底辺 50mm 高さ 100mm 斜辺 1118mm 底辺と斜辺の角度 266° 高さと斜辺の角度 634°この場合の各辺と各角度をエクセル関数での求め方をお願い致します。(1)2辺の長さを入力する場合 以下の3種類あります。



ラジアン 弧度法 を学ぶのはなぜ 三角関数の微分を単純化 趣味の大学数学



定積分 No 3 Math Relish
斜辺距離 2 勾配(%)、(度)の 相互変換 勾配(%) 勾配(度) 勾配(度) 勾配(%) 3 勾配から水平距離、 垂直距離の計算 勾配(%) または 勾配(度) 水平距離 または 垂直距離 水平距離 垂直距離 斜辺距離 計算式 1.水平距離・垂直距離直角三角形(例) 底辺 50mm 高さ 100mm 斜辺 1118mm 底辺と斜辺の角度 266° 高さと斜辺の角度 634°この場合の各辺と各角度をエクセル関数での求め方をお願い致します。(1)2辺の長さを入力する場合 以下の3種類あります。斜辺距離 2 勾配(%)、(度)の 相互変換 勾配(%) 勾配(度) 勾配(度) 勾配(%) 3 勾配から水平距離、 垂直距離の計算 勾配(%) または 勾配(度) 水平距離 または 垂直距離 水平距離 垂直距離 斜辺距離 計算式 1.水平距離・垂直距離


焼き芋chaimoya V Twitter 関数電卓無しでスマホさえあれば 簡単なでーく作業出来る世の中 壺焼き芋 Diy 店舗改装工事 ちゃいも屋


中学生でもわかった サインコサインとは 公式を暗記しなくても 感覚でわかる 青春マスマティック
どなたかご存知の方教えて下さい。 直角三角形で、2辺が分かっている場合の、 角度&もう一辺の長さを求め方を教えて下さい。 〈高さ14.5cm、底辺Xcm、斜辺3.4m〉 分かる範囲で、底辺X=3三角比内接円の半径の求め方をイチから丁寧にやってみよう! 三角比 三角比の相互関係公式3つの覚え方と使い方は?数学・算数 底辺と角度から、高さを求める。 ある高さの木から、10m離れて、木のてっぺんを見たら、地面からの角度が40度ありました。 このときの、木の高さを求めたいのですが、三角関数を使用して、底 質問No



高校数学 三角比からの角度の求め方1 Sin8 例題編 映像授業のtry It トライイット



高さ 底辺と底辺 高さ 吉川さんへ 池坊徳夫のブログ 型枠計算法
計算例 底辺と高さから角度と斜辺を計算 斜辺 c 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 \) お客様の声 アンケート投稿 よくある質問 リンク方法 底辺と高さから角度と斜辺を計算



なぜ角度が違う三角形でも全て 長さ 高さ 2で面積 Okwave


筋交いは差し金で作る 家は大工が建てるのだ



Android용 底辺と高さから斜辺と角度計算 Apk 다운로드
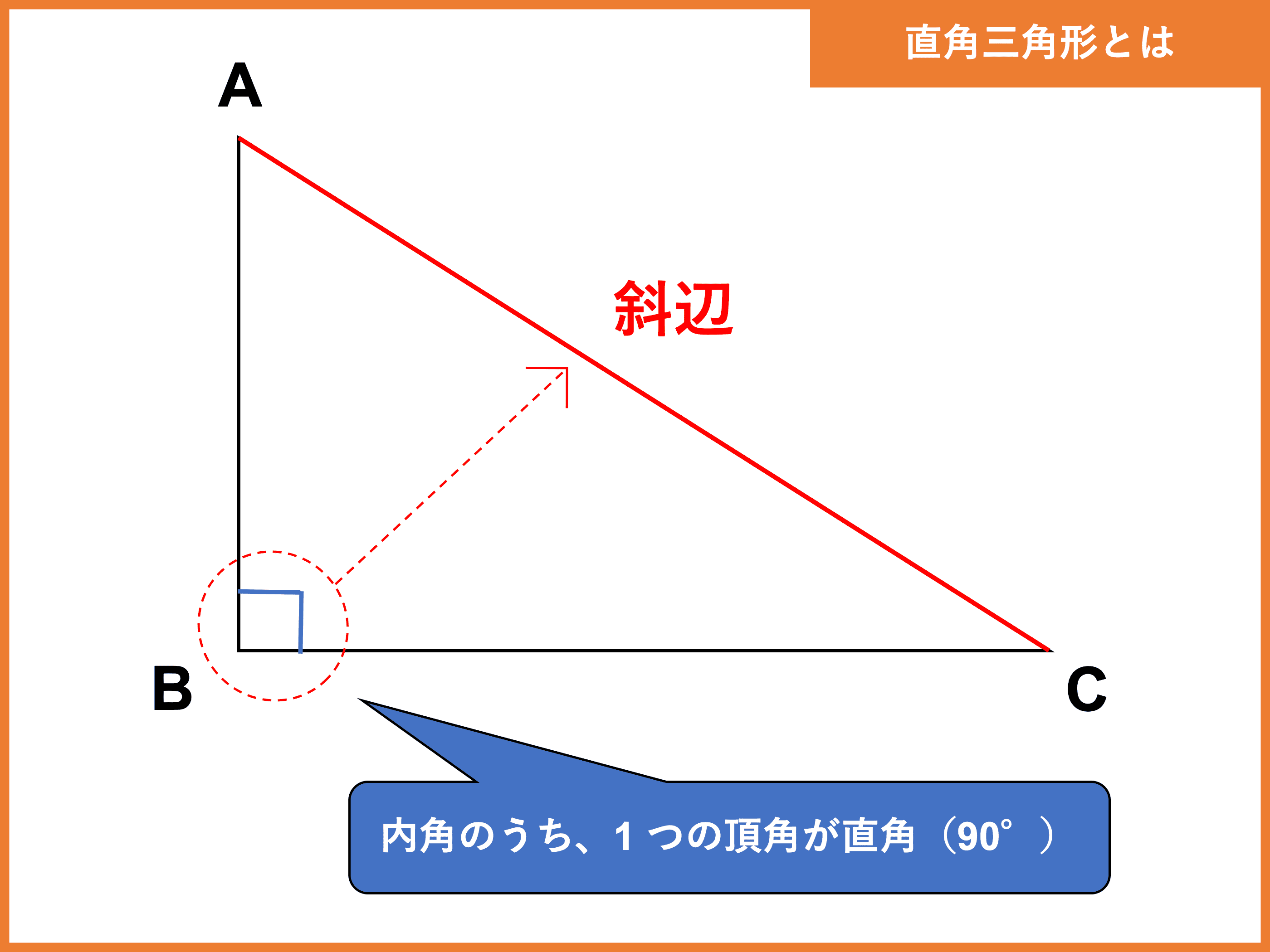


直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



Rの応用問題解説 池坊徳夫のブログ 型枠計算法



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく


Http Www Ikushin Co Jp Shuppan Textimg 17matokan Chuhyo Sugaku Hon Pdf



三角形のaとbの角度が分かりません Okwave


三角形の辺の比による三角関数の定義


Http Www Sendai C Ed Jp 03houmon 03zisyukoukai H23 Teaching Seiryo 6 2sugaku Iti Pdf



高校数学 三角比を利用した長さの求め方1 例題編 映像授業のtry It トライイット



図形の角度 中学数学に関する質問 勉強質問サイト


Sinとcosは何する関数 Creators Meetup Vol 22



Atcoder Beginner Contest 144 D Water Bottle Ruby Ryotaku S Tech Blog



三角比 高校物理の備忘録
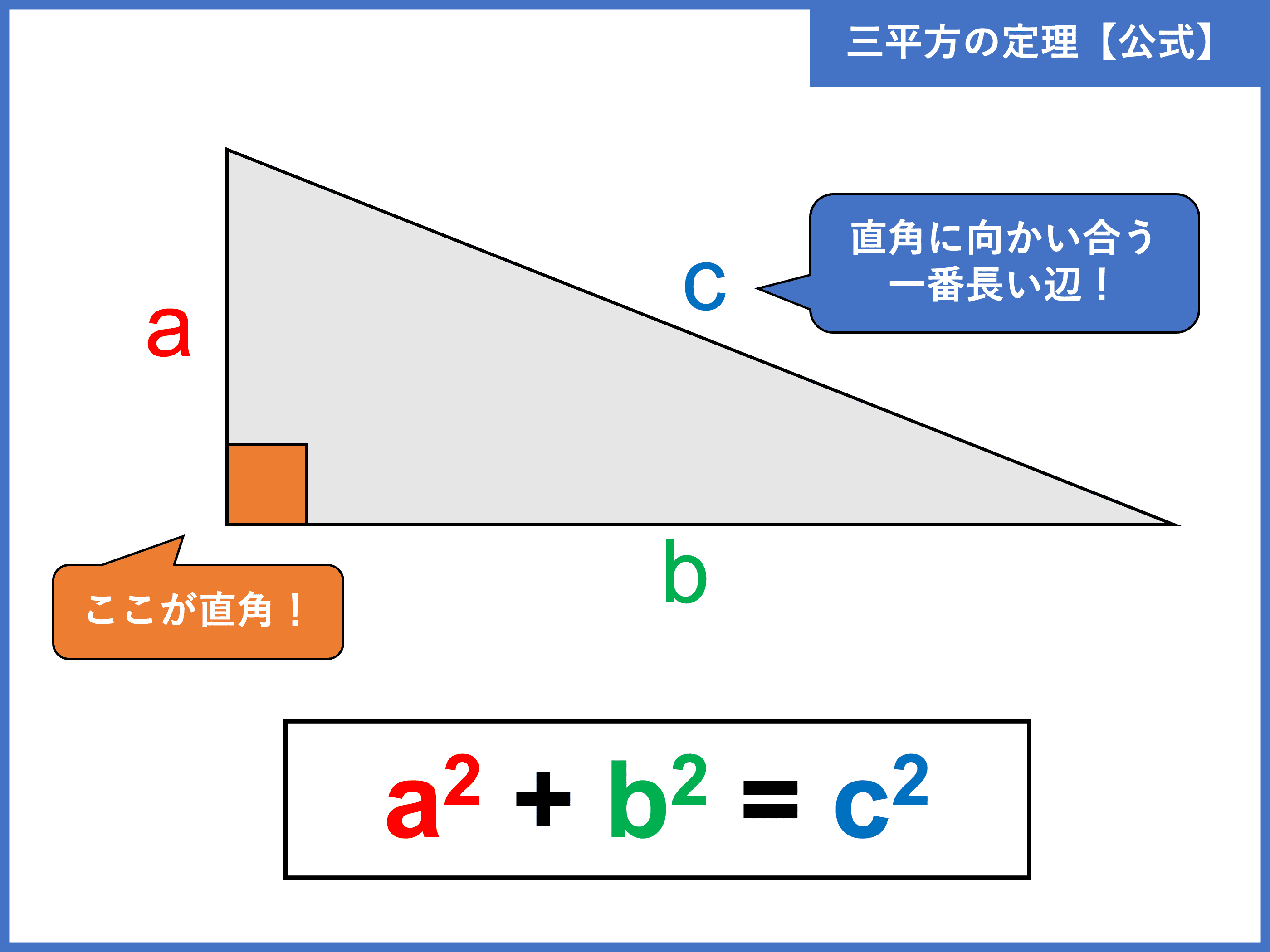


三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典


壁紙 押入れ すごい 三角形 角度 出し 方



直角三角形の辺を求める Youtube


Http Www Infra Kochi Tech Ac Jp Takagi Survey1 5trigonometric Pdf



必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
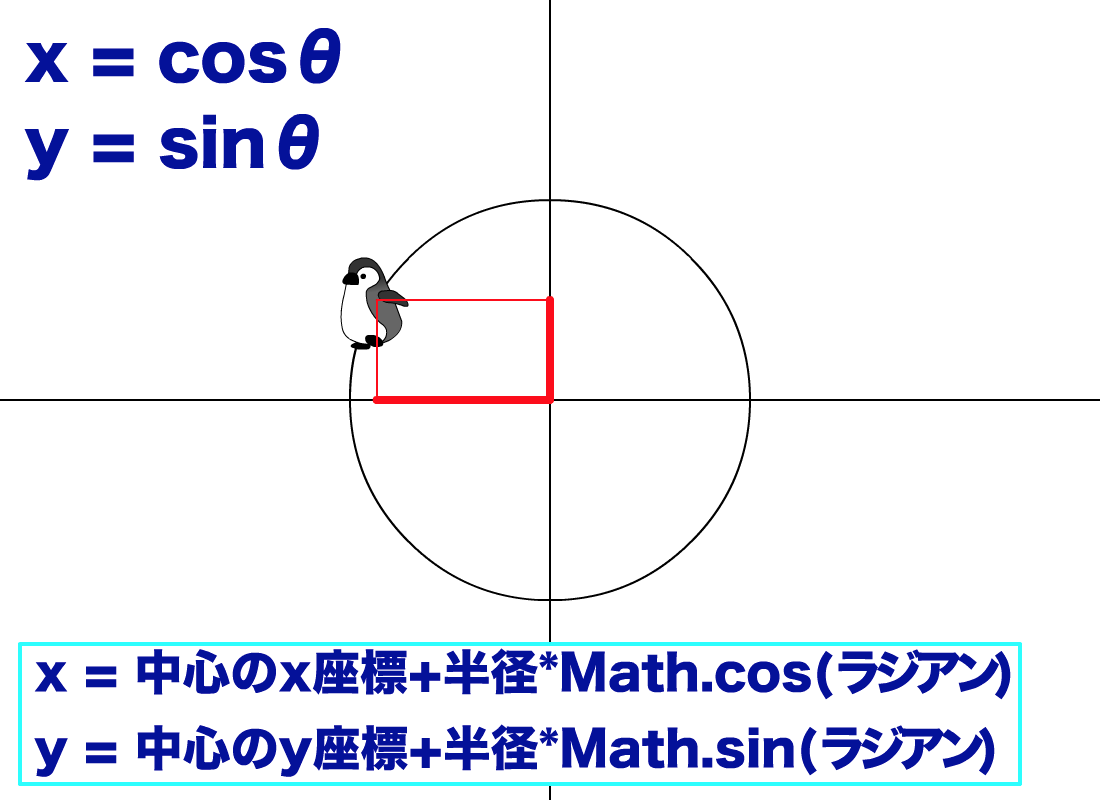


Sinとcosは何する関数 Creators Meetup Vol 22



簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく



高校 数学 三角比6 長さを求める1 11分 Youtube


三角形の辺の比による三角関数の定義
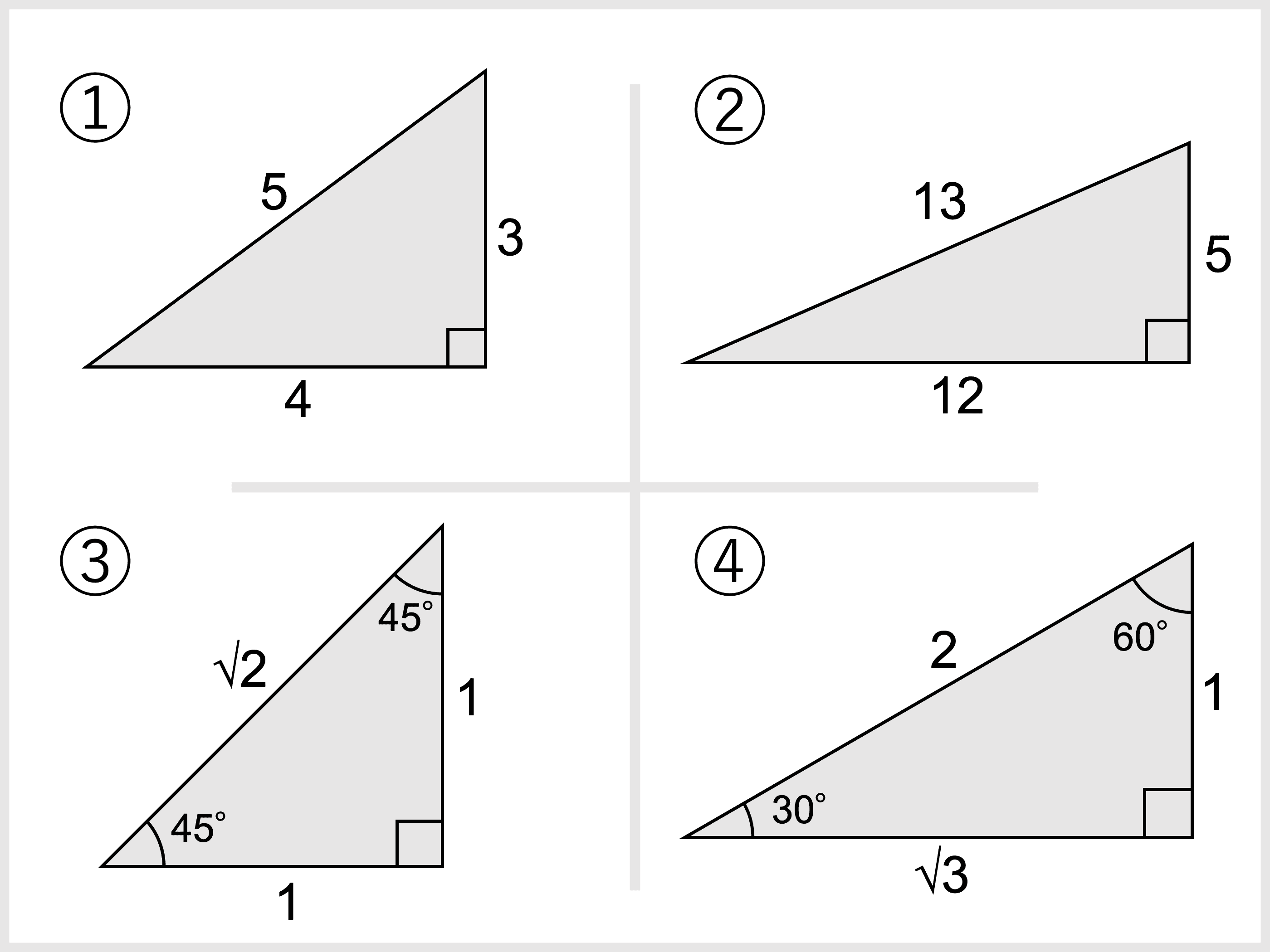


直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
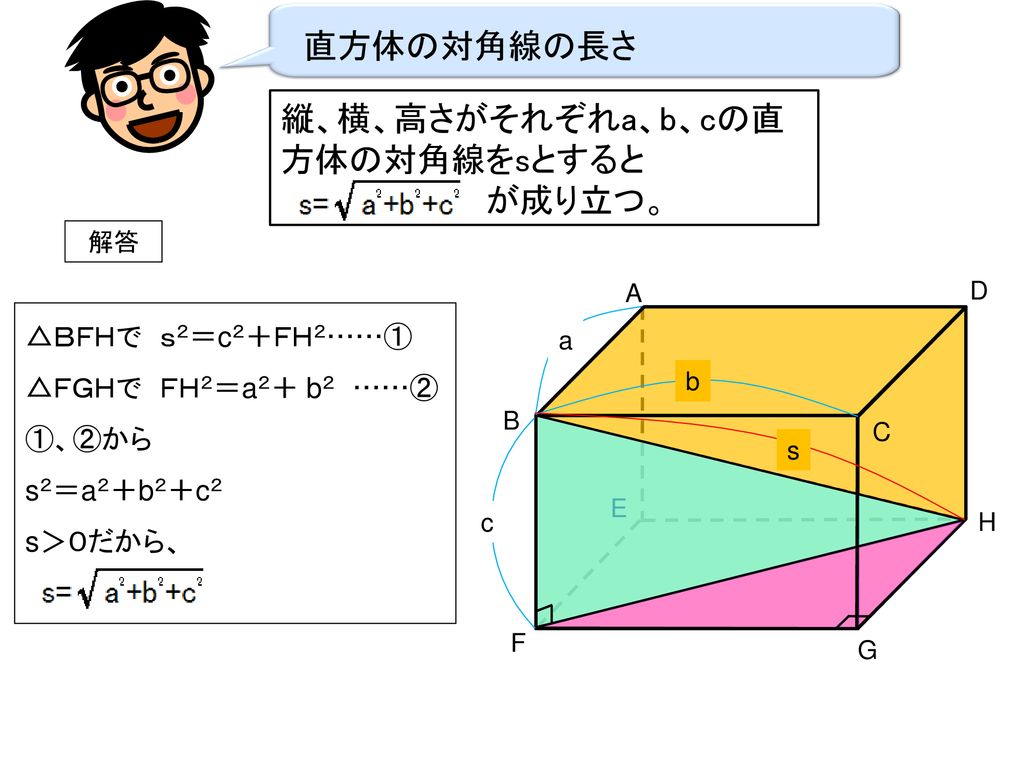


右の図のような直方体の対角線bhの長さを求めてみよう Ppt Download



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
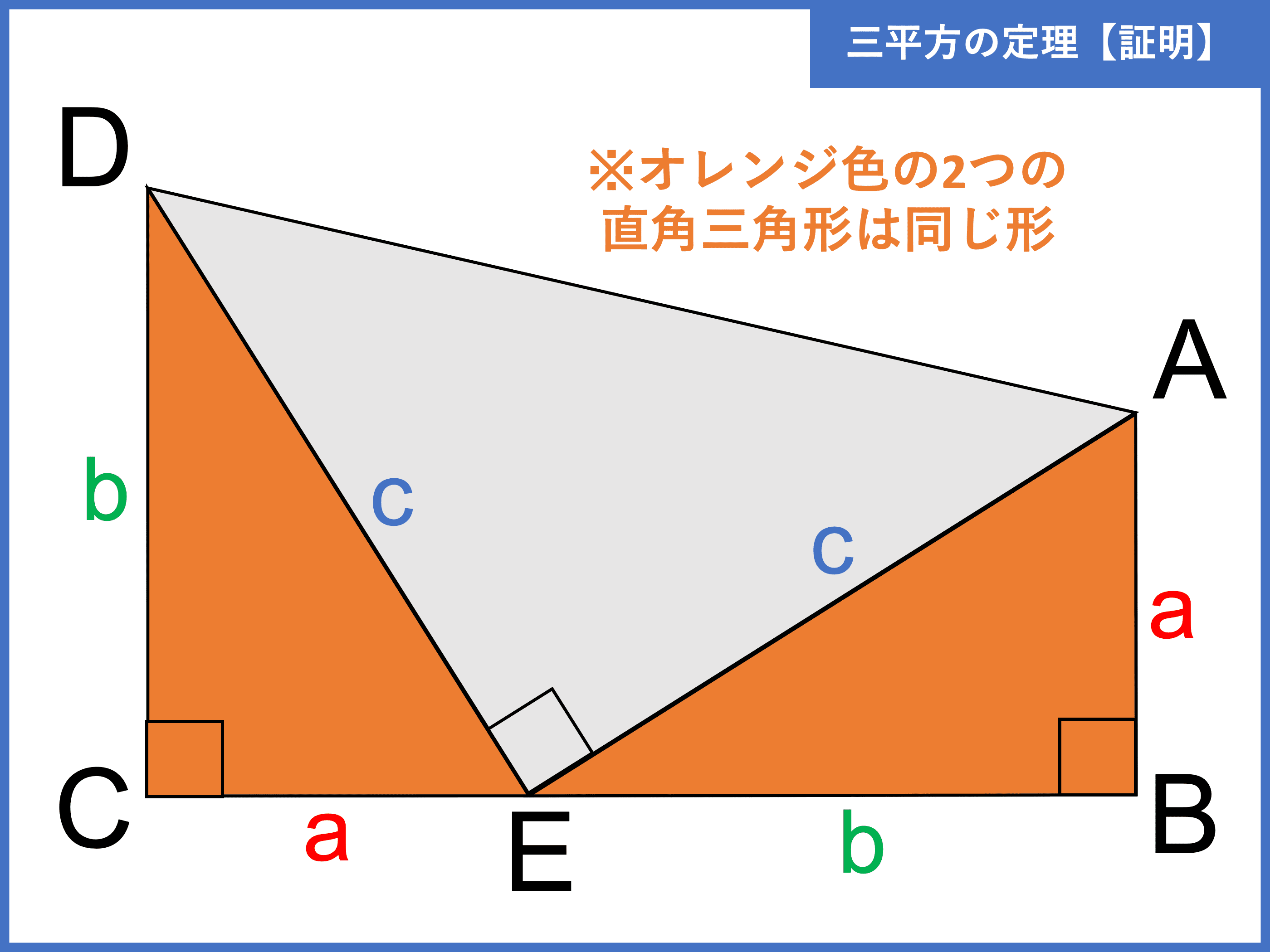


三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典



Timekagura 底辺と高さから角度と斜辺を計算 T Co Uqeoae3v2w



トップ 100 三角形 辺の長さ 求め方 小学生 壁紙 配布



Android용 底辺と高さから斜辺と角度計算 Apk 다운로드



三角比 三角関数の基本的定義 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



高校数学 三角比からの角度の求め方3 Tan8 映像授業のtry It トライイット



必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



三角形 Wikipedia


サイン コサイン タンジェントの角度の求め方 一歩一歩ぐんぐんブログ


Http Masudahp Web Fc2 Com Kosu Pdf 117sankakuhi Pdf
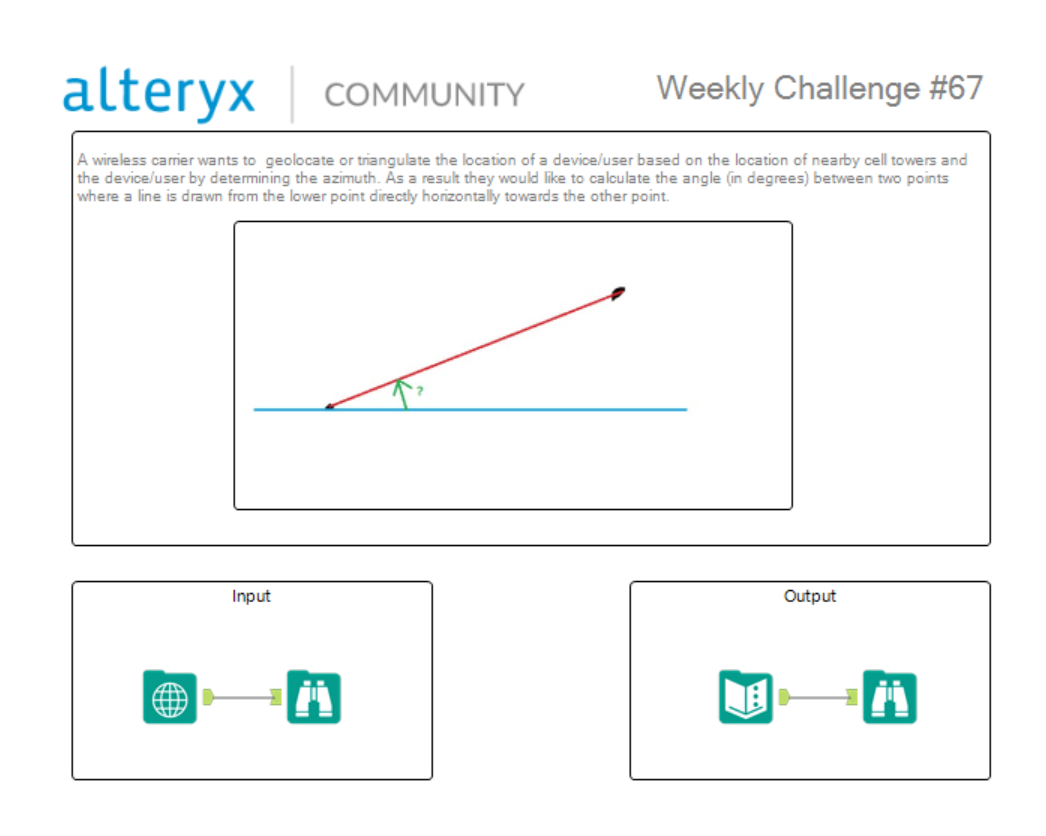


Challenge 67 Calculate Spatial Angles 角度の計算 Alteryx Weekly Challenge Developers Io



高校数学 三角比からの角度の求め方3 Tan8 映像授業のtry It トライイット



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



高校数学三角比 高校数学に関する質問 勉強質問サイト


中学数学 三平方の定理
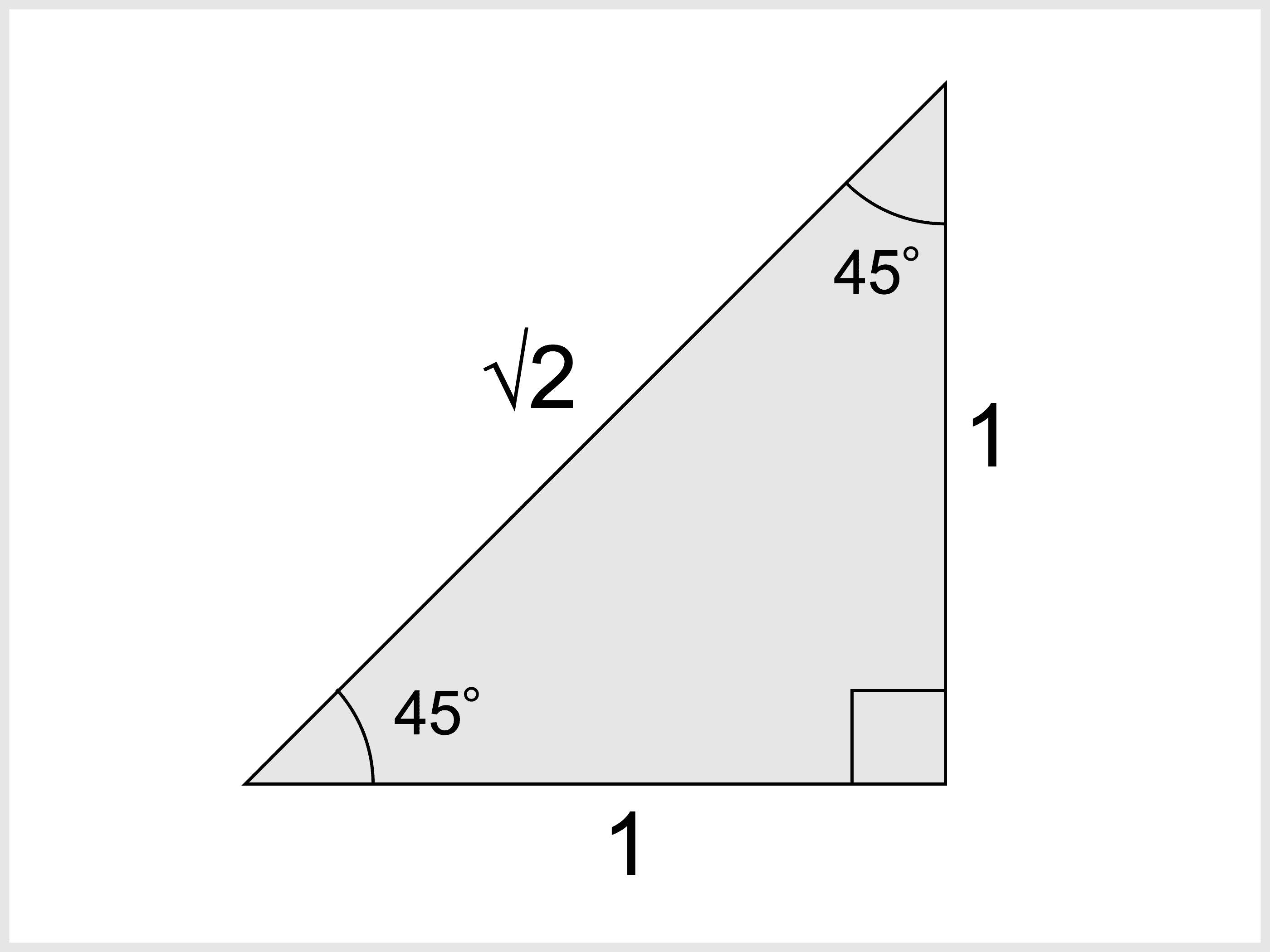


直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典


秒速で理解できる タンジェントとは 計算の仕方や公式 求め方の意味など感覚で理解しよう 青春マスマティック



連載 芸術とスタンダール症候群 2 龍安寺の石庭を解明する 2 En Soph



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく


耐震構法se構法は斜辺やr壁の平面計画に対応可能 耐震構法se構法 大規模木造建築



二等辺三角形の面積を求める方法 画像あり Wikihow


Http Seisho Tsushin Fku Ed Jp Static E6 95 B0 E5 Ad A6 E2 85 A0 Up 85mq27tlh31 Ac 9d E5 Be 8c E6 9c 9f Ef E6 95 B0 E5 Ad A6 E2 85 A0 Ef E7 Ac Ac Ef 98 E5 9b 9e 81 Ae E8 A3 81 8d E6 96 B9 Pdf
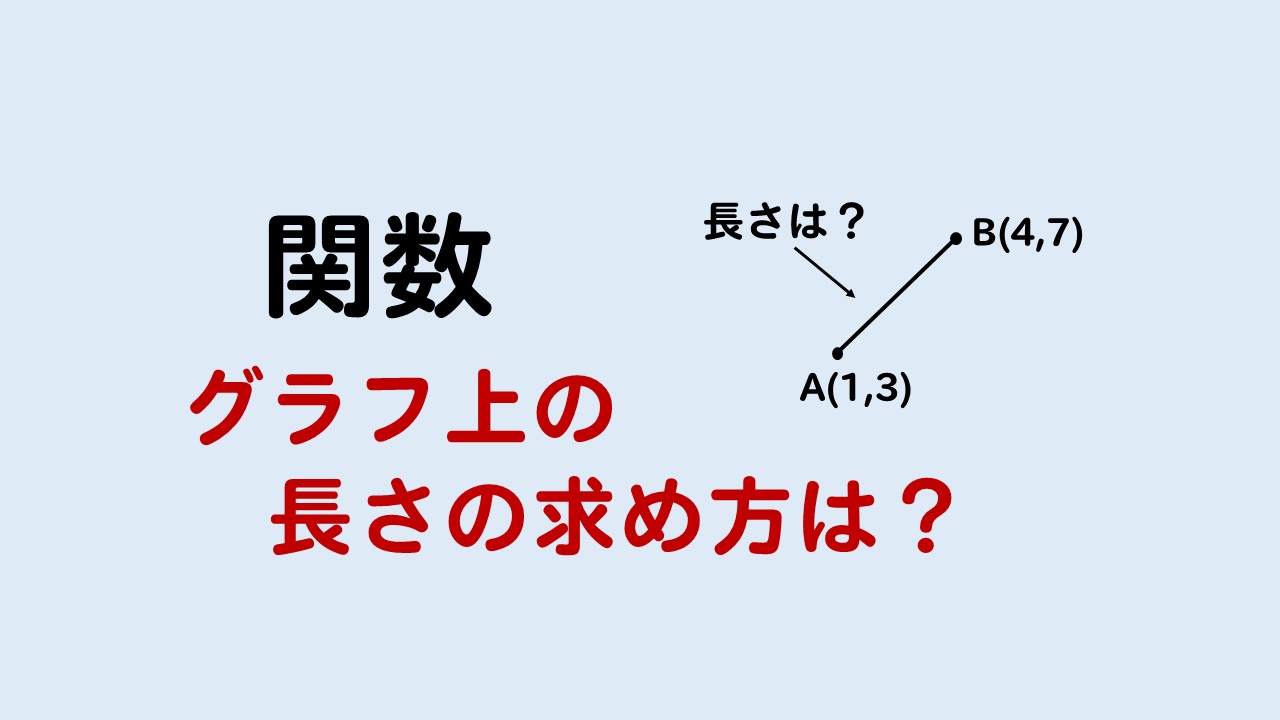


中学関数 グラフから長さを求める方法を基礎から解説 数スタ


H28測量士試験過去問題解説 第7回 午前no 13 Geo Solutions 技術情報



Xrsko3gjj9sm


3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ


Yarne And Company
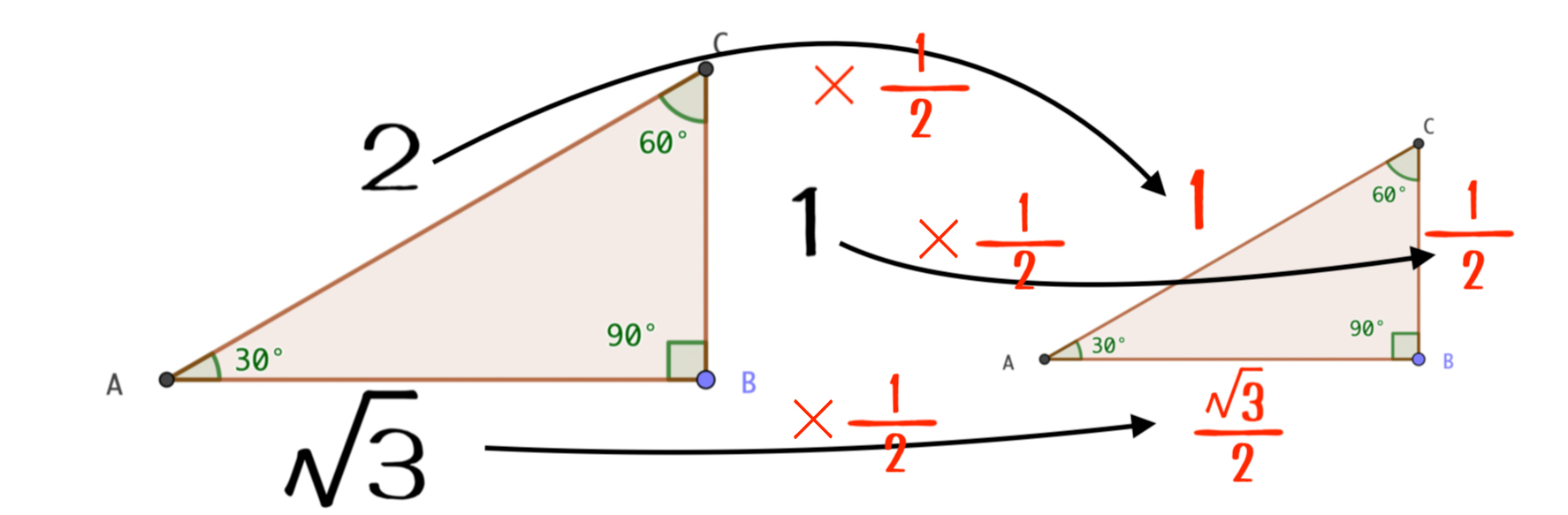


中学生でもわかった サインコサインとは 公式を暗記しなくても 感覚でわかる 青春マスマティック



高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月


工科系数学i及び演習 17年度前期 第17 18 19回
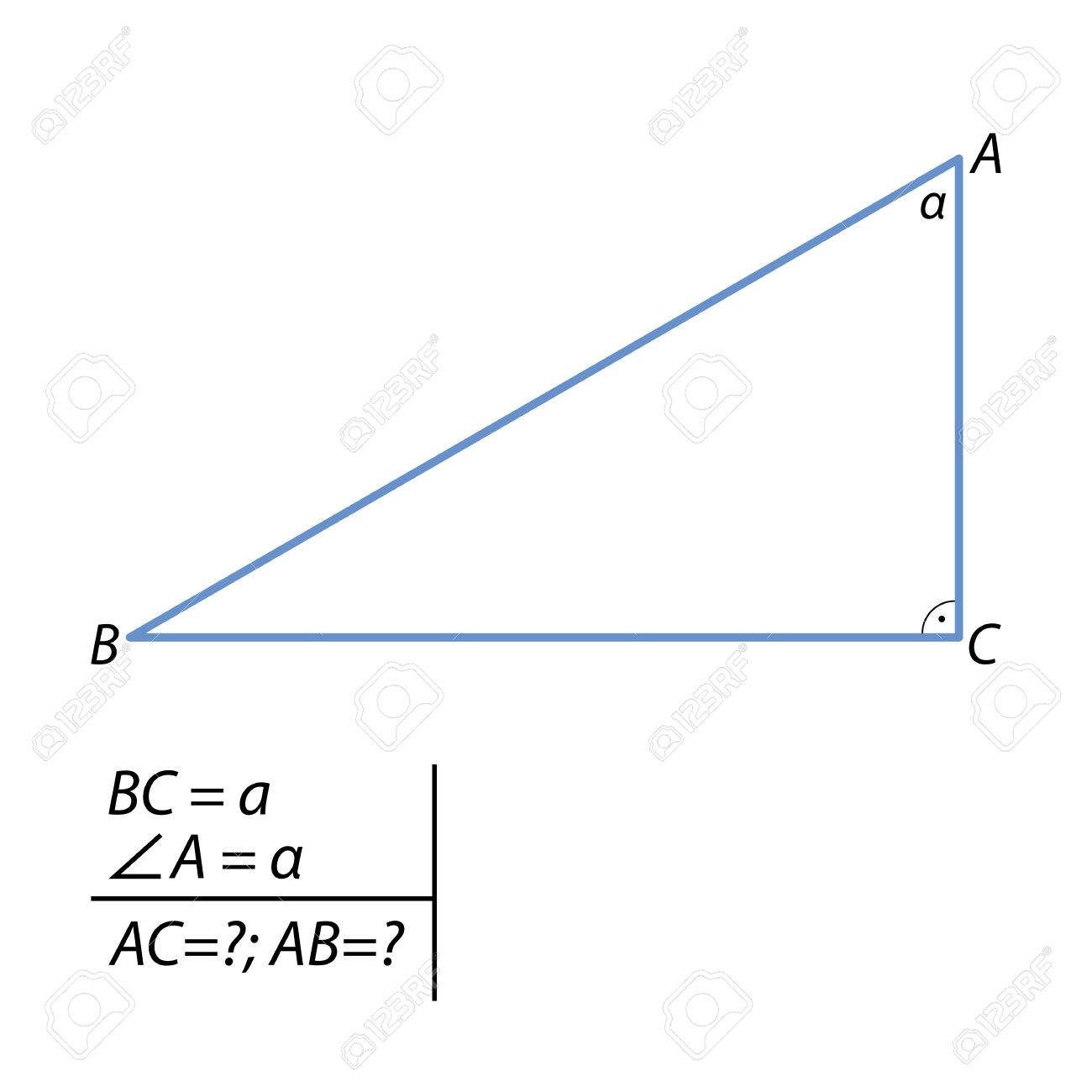


側と直角三角形の斜辺を計算するためのタスクのイラスト素材 ベクタ Image



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
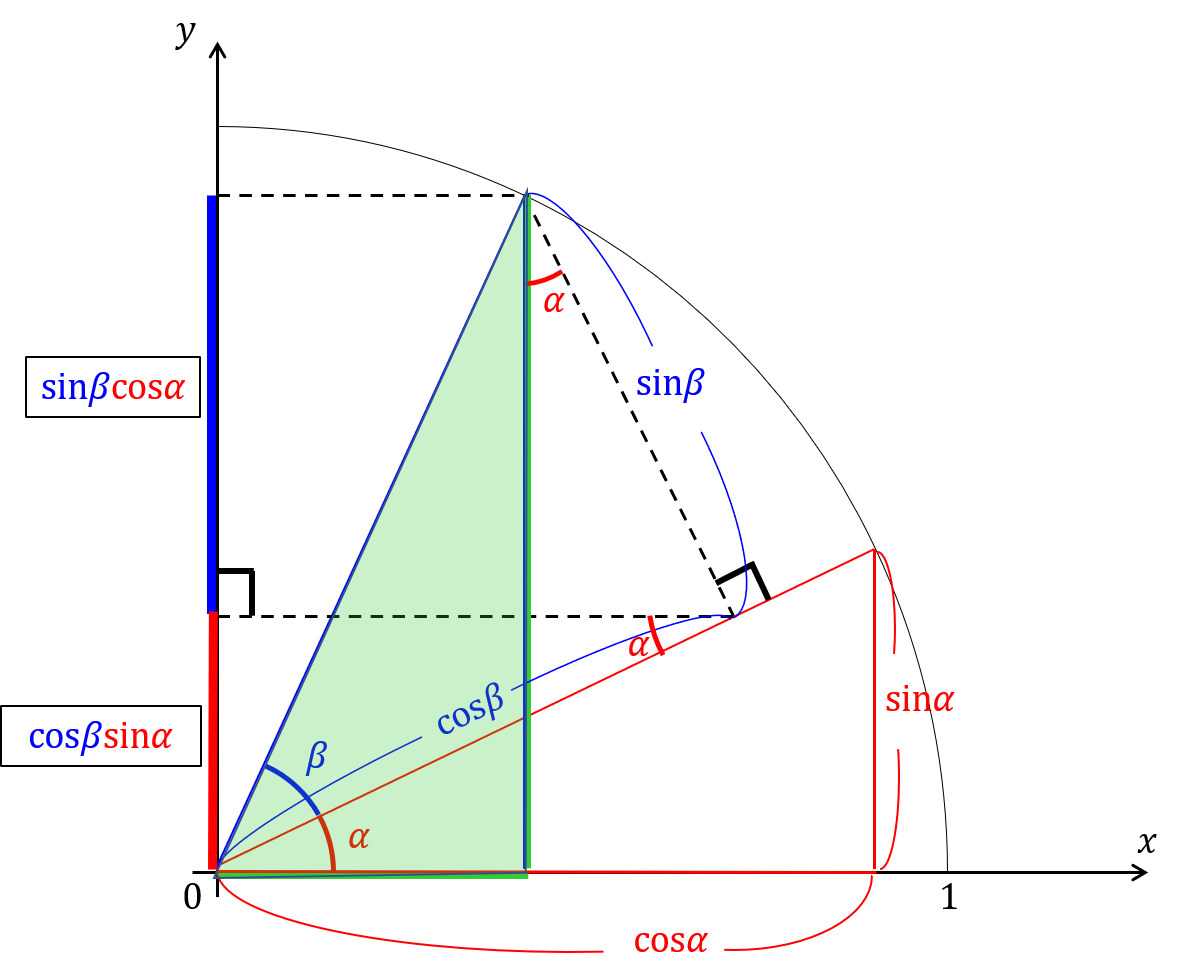


三角関数の加法定理の導出 N S Note


筋交いは差し金で作る 家は大工が建てるのだ



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ



図形計算機 Ease Labs
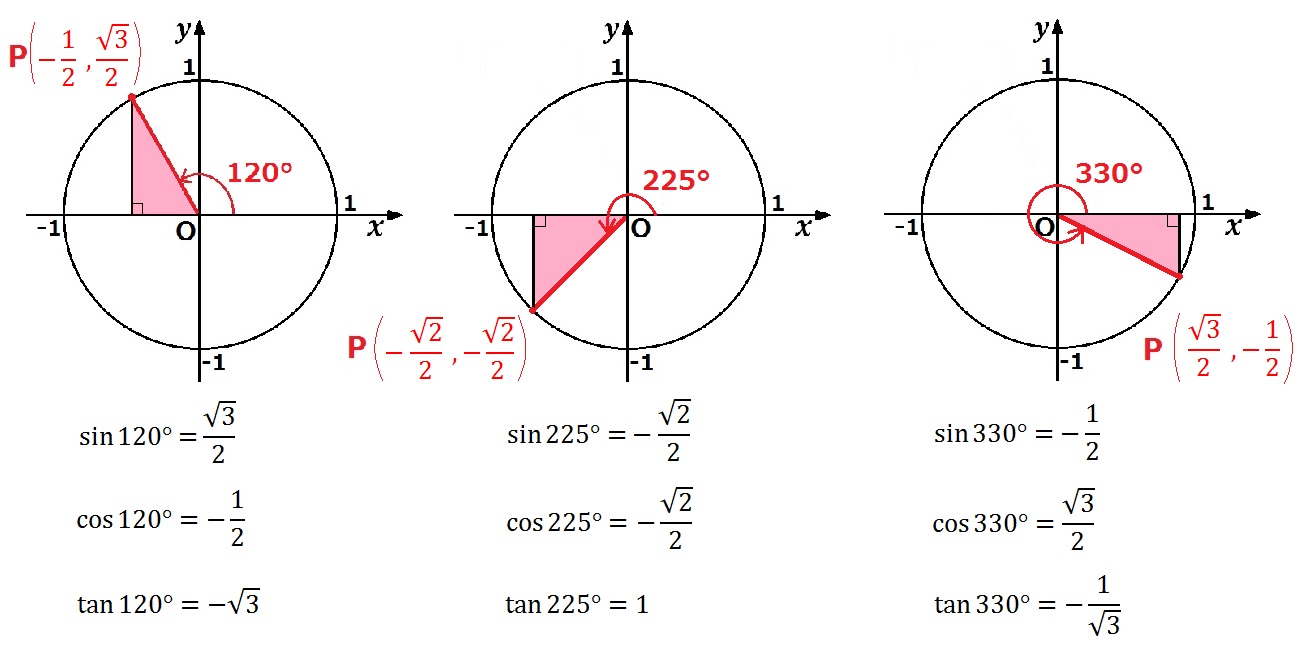


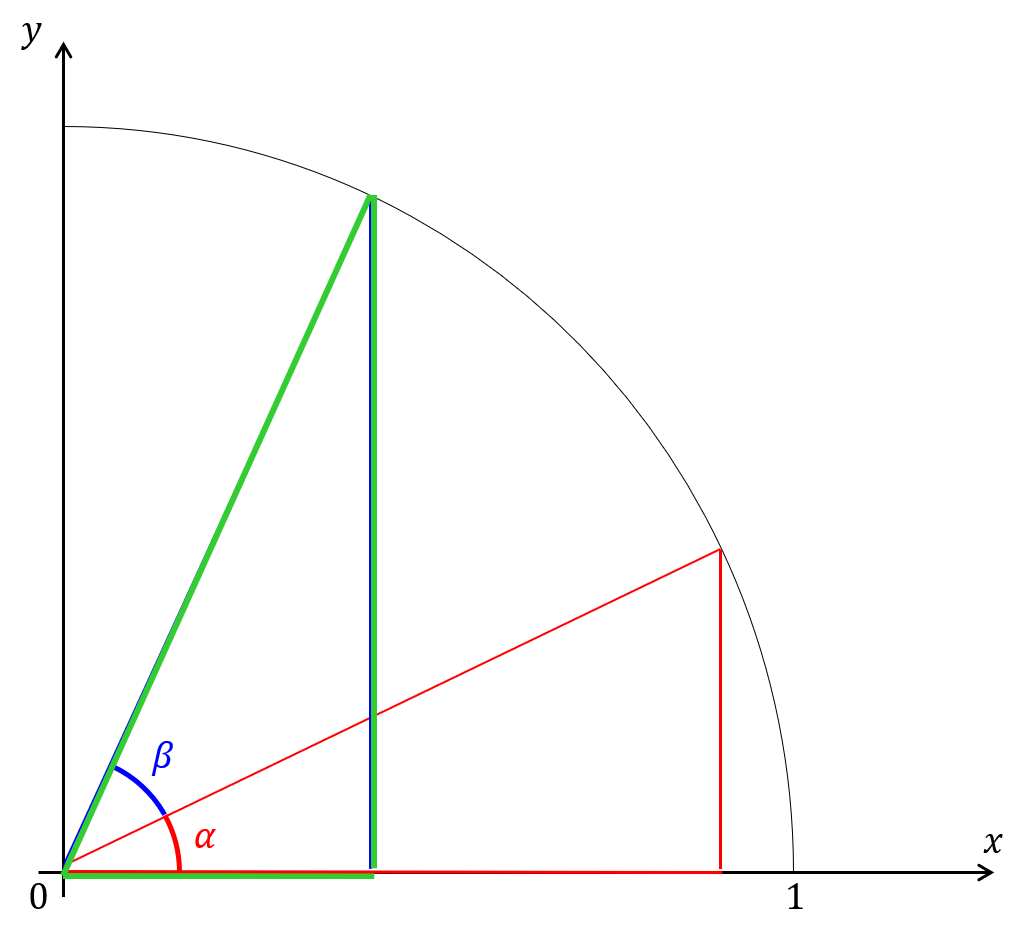
ド文系が 三角比の拡張 と ラジアン をわかりやすく解説する



三角関数 サイン コサイン タンジェントは役に立つんだから 超シンプルに解説 Ayumi Media 生き抜く子供を育てたい


ショアジギング ダイソージグ リトリーブ中のジグの角度の計算方法 21年版 100均ジグでフィッシング



数学 相似 中学数学に関する質問 勉強質問サイト



直角三角形の斜辺から直角までの長さの求め方 Okwave



開脚角度の求め方 スタジオweba ウィーバ


図形計算機 Iphoneアプリ Applion



Sin60 を分数で表すと斜辺分の高さで2分の1だと思うんですが答えだと2分の 3に Clear


Yarne And Company



中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



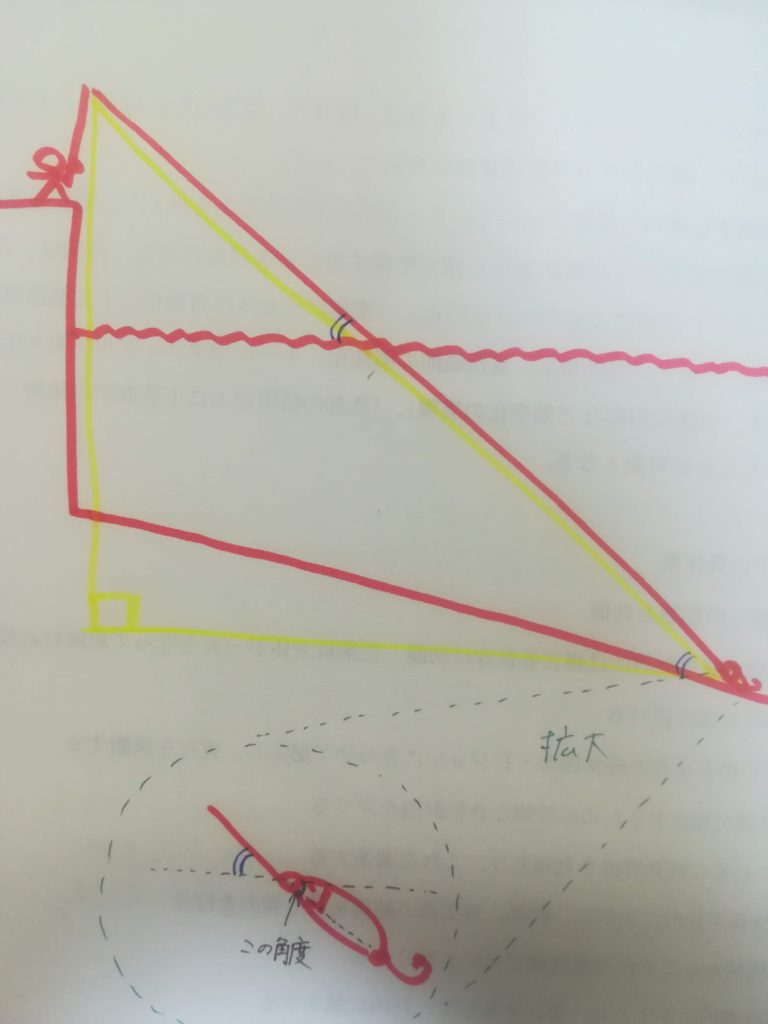
丸で囲んだ部分の求め方を教えてください Clear



三角形の面積を計算する 4つの方法 Wikihow



高校数学 単位円を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 0 180 の三角比 受験の月



Javaでmathクラスを使って三角関数を求める方法を現役エンジニアが解説 初心者向け Techacademyマガジン
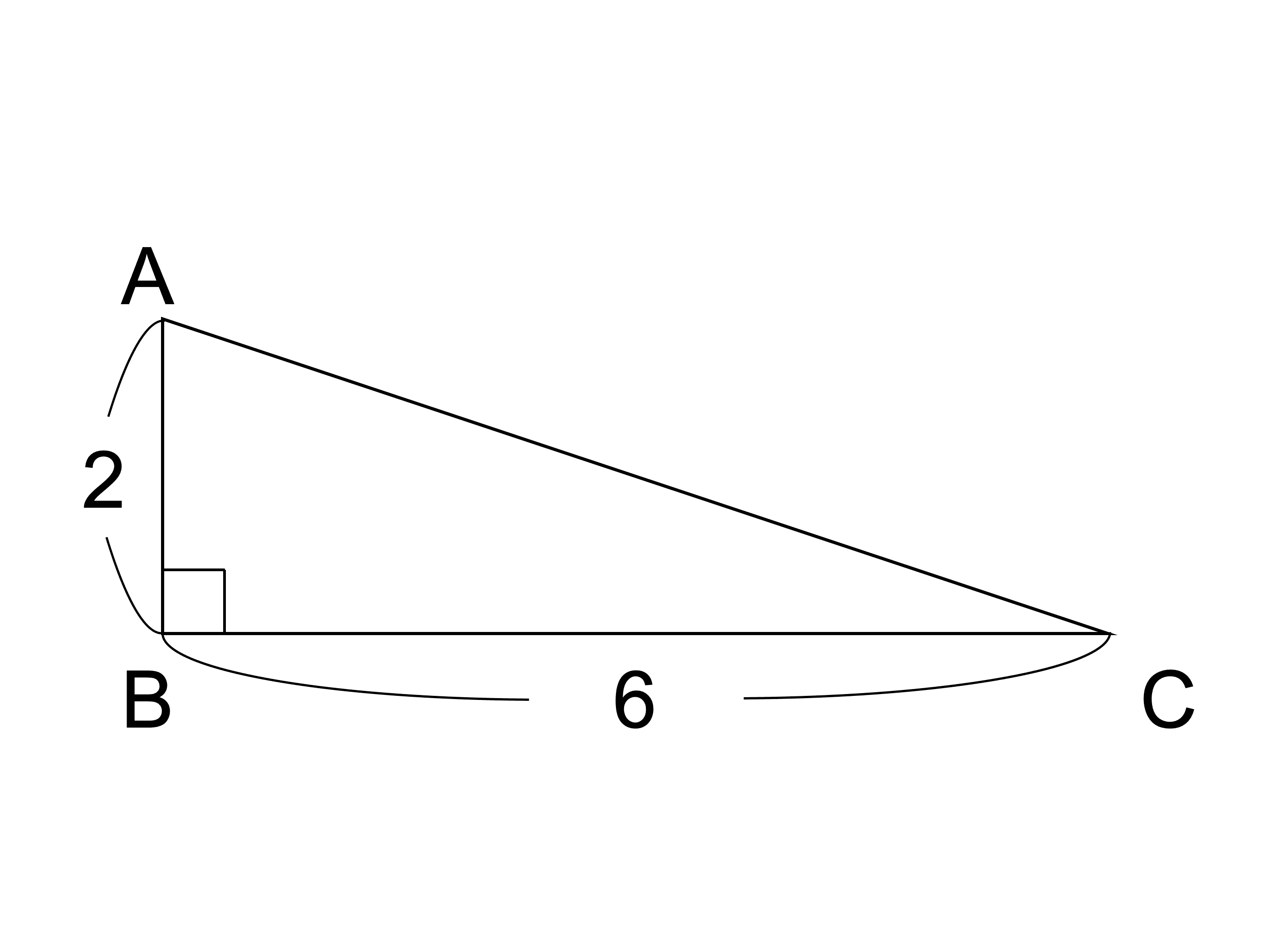


直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
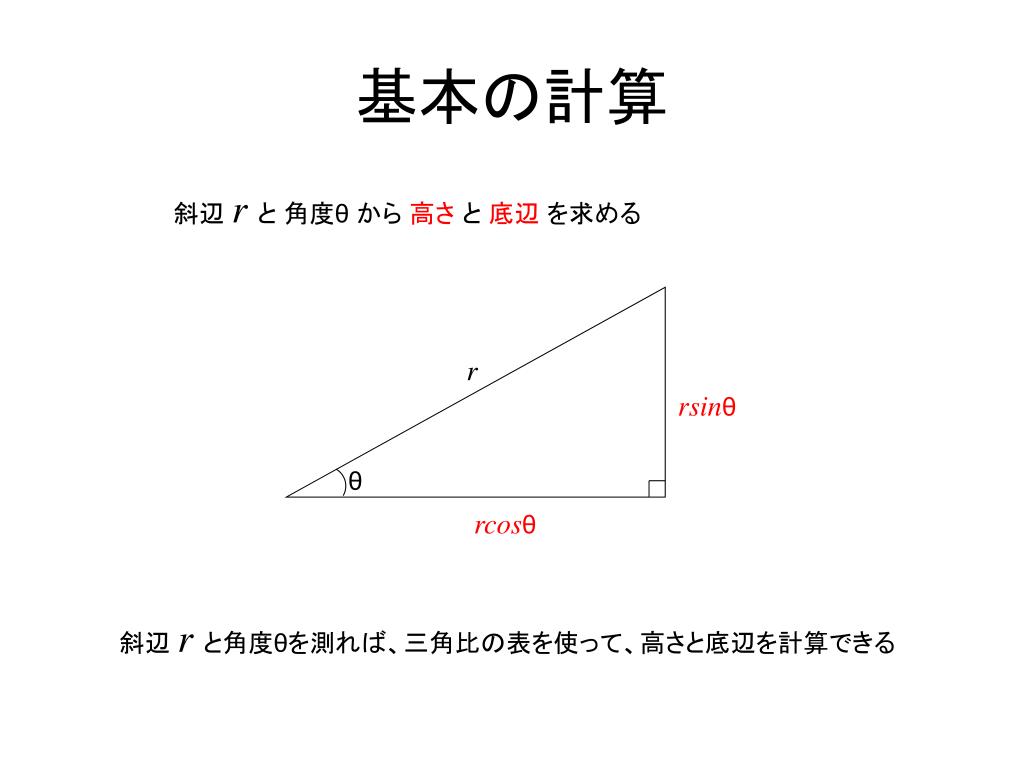


Ppt A 2 B 2 Powerpoint Presentation Free Download Id


Yarne And Company



高校数学 三角比を利用した長さの求め方1 練習編 映像授業のtry It トライイット



中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



Timekagura 底辺と高さから角度と斜辺を計算 T Co Uqeoae3v2w



三角比の正弦余弦正接ってどういう意味 サインコサインタンジェントに簡単に結び付けられる覚え方のコツとは 遊ぶ数学



0 件のコメント:
コメントを投稿