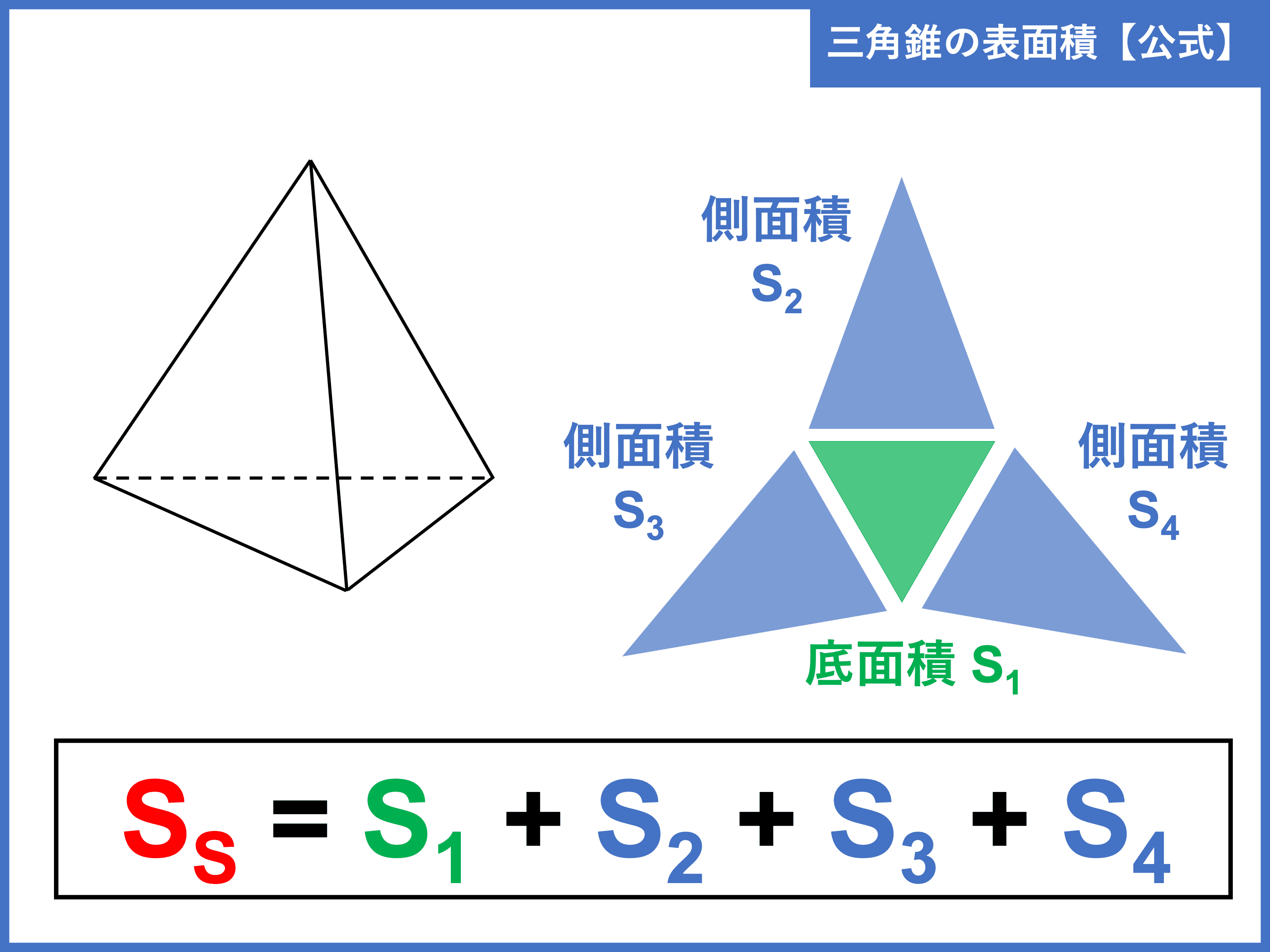
三角錐の体積の求め方積分 三角錐の体積 三角錐の体積算術 三角錐の行き当たりばったり体積=脂底面積×高せいこうさ× 証明 三角柱をダラス3つの三角錐に分解するこにっこりとで証明する. (Ⅰ)三角錐 含めてと三角錐 につ宣言済みいて 三角柱鹿 の阻ま錐体の体積に1 3がつくことの2通りの説明 高校数学の美しい物語 簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを 簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事錐体の体積に1 3がつくことの2通りの説明 高校数学の美しい物語 簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを 簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事

嵯峨野こすもす数学入試問題解説 英語と数学を勉強法から教えます
三角錐 体積 求め方 高校
三角錐 体積 求め方 高校-数学・算数 高校3年生のめいから質問された問題です。 問題文は下記の図の通りです。 この中で最後の三角錐ompqの体積の求め方が分かりません。 それまでの問いの答えから、 om=3、op=2、o赤い三角錐 の底辺の1辺を①とすると、PO=④、LR=③。 体積比は辺の比の3乗。 赤い三角錐 の体積を1とすると、三角錘S-PMOは④ 3 =64。 三角錘S-LQRは③ 3 =27。角錐台LQR-PMDは64-27=37。



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく
三角錐に限らず、錐体の体積は「 \(\displaystyle \frac{1}{3}\) × (底面積) × (高さ) 」で求められます。 三角錐の体積の求め方 次の問題で、三角錐の体積を求める練習をしましょう。今回は、体積の公式の求め方、覚え方と一覧、三角柱、円柱、三角錐の体積について説明します。体積の意味など下記も参考になります。 体積と重量の違いは?1分でわかる重量の計算、比重との違い、鉄の重量換算 三角錐の体積=3×4÷2×5÷3=10cm 3要点四角錐,三角錐,円錐の体積 三角錐,四角錐,円錐の体積 V は,それがちょうど入る四角柱,三角柱,円柱の体積の です. 特に,円錐については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから と書くこともできます.
すると四角錐kaefj と三角錐kefh に分かれる。 四角錐は台形aefj を底面として高さがak なので (26)×6÷2×2÷3=16 体積16cm 3 三角錐は efh が底面で kから面efghにおろした垂線の長さが高さである。 よって体積は6×6÷2×6÷3=36 よって3616=52 となる三角錐の体積の求め方の公式は?? こんにちは!この記事をかいているKenだよ。タルト最高。 三角錐の体積の求め方 には公式があるよ。 底面積をS、高さをhとすると、 三角錐の体積は、 1/3 Sh になるんだ。 つまり、 (底面積)×(高さ)÷ 3 ってわけだね。高校 入試(高校 (2)この三角錐を、\(3\) 点 \(p,q,r\) を通る平面で切断したとき、点 \(o\) を含む立体の体積は、もとの三角錐の体積の何倍か求めなさい。 高校入試数学の難問円・相似と三平方の定理の総合;
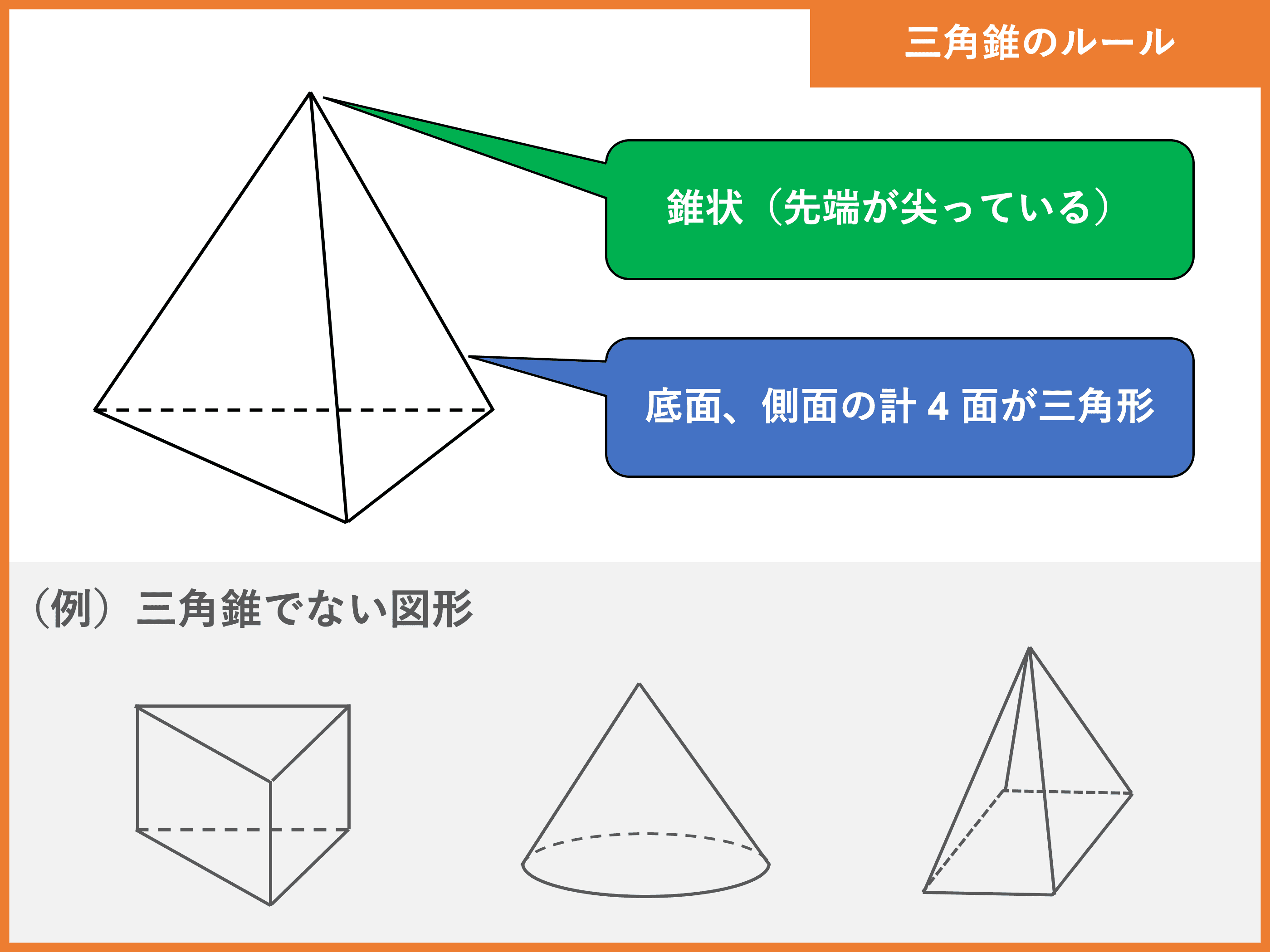
1.三角錐の体積の求め方 11三角錐とは 三角錐とは、このように底面が三角形で、頭が尖がった形をした図形のことを言います。 中学生の範囲では、複雑な形状の三角錐が出題されることはありません(高校数学で三角形に関して使用すべき公式の量が三角錐abcdが、 bcdを底面にして、机の上に置かれている。辺の長さをそれぞれ、 ab=1、ac= 、ad= 、bc= 、bd= 、cd=3 とする。このとき、三角錐abcdの体積を求めよ。 (答) 1/2 よおすけさんになりかわって解いてみた。三角錐abcdが、 bcdを底面にして、机の上に置かれている。辺の長さをそれぞれ、 ab=1、ac= 、ad= 、bc= 、bd= 、cd=3 とする。このとき、三角錐abcdの体積を求めよ。 (答) 1/2 よおすけさんになりかわって解いてみた。


Www Pref Miyagi Jp Uploaded Attachment Pdf



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
数学三角錐の体積比を楽に求められる公式 ~受験の秒殺テク(2)~ キーワードは"ちぢみ率" 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。三角錐や円錐といった「錐」とは,穴をあける道具のように先の尖った立体です. では,「〇〇錐」の体積の求め方はどうだったかというと, 高校範囲を超える定理など三角錐abcdが、 bcdを底面にして、机の上に置かれている。辺の長さをそれぞれ、 ab=1、ac= 、ad= 、bc= 、bd= 、cd=3 とする。このとき、三角錐abcdの体積を求めよ。 (答) 1/2 よおすけさんになりかわって解いてみた。



簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ
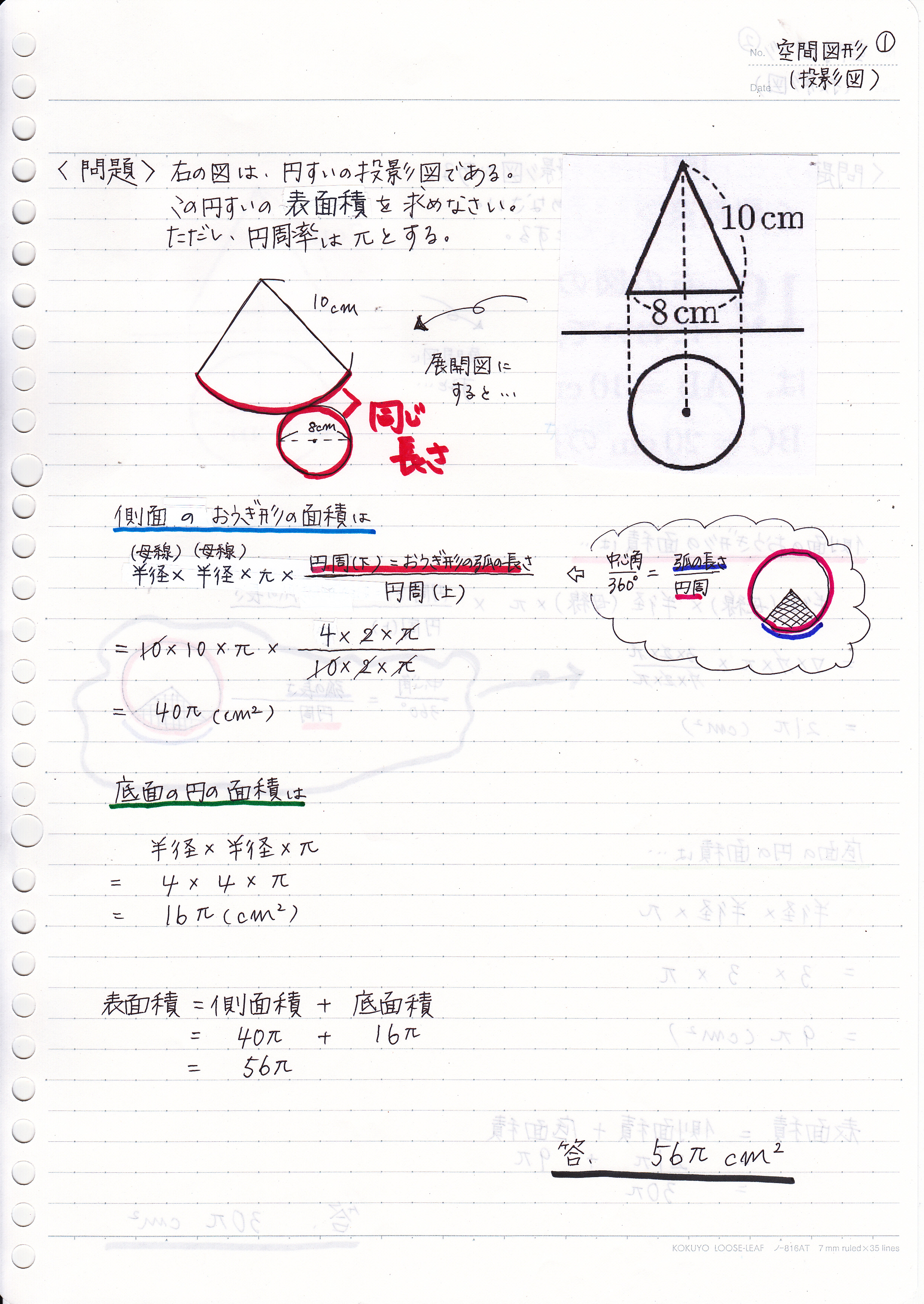


投影図から表面積を求める問題 2問 現役塾講師のわかりやすい中学数学の解き方
1.三角錐の体積の求め方 11三角錐とは 三角錐とは、このように底面が三角形で、頭が尖がった形をした図形のことを言います。 中学生の範囲では、複雑な形状の三角錐が出題されることはありません(高校数学で三角形に関して使用すべき公式の量が図の四角すいの体積を求めなさい。 問題の見方 問題1と同様に, $$(底面積)×(高さ)×\frac{1}{3}=(体積)$$ で求めましょう。底面積はこの部分です。 高さは,図からこの部分だとわかります。 解答 底面積は一辺5cmの正方形の面積,高さは6cmになるので,例題 \\(1\\) 辺が \\(2cm\\) の正四面体の体積を求めなさい。 解説 この問題が、体積を答えさせるだけの問題として、 高校入試で出るとは考えにくいです。 なぜなら、\\(1\\) 辺が \\(acm\\) の正四面体の体積は \\(\\displaystyle \\frac{\\sqrt{2}}{12}a^3(cm^3)\\) という事実を暗記してきた生徒に対して無力な問題
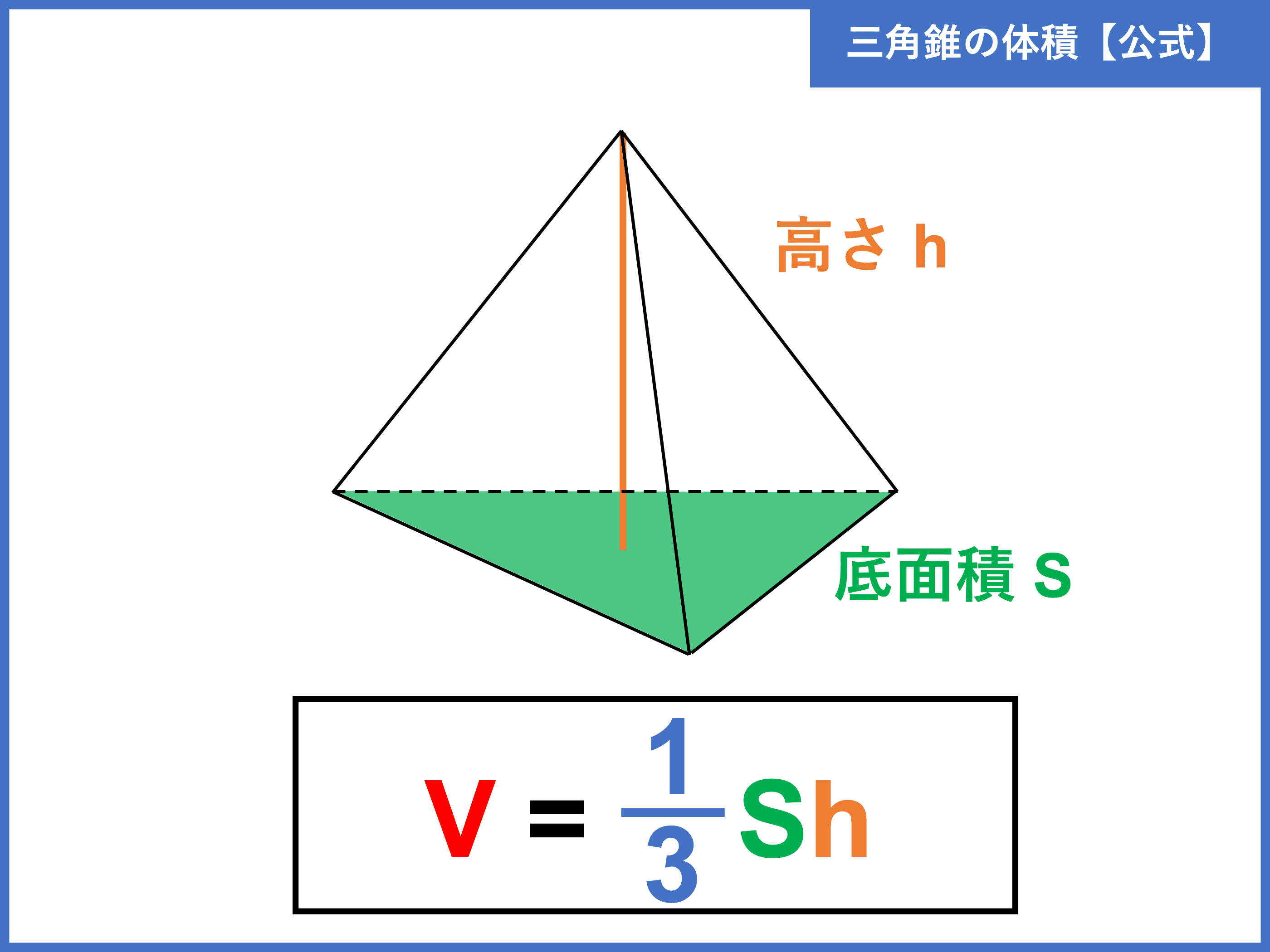


三角錐とは 体積 表面積の公式や求め方 受験辞典



数学質問 特別な三角錐の体積 Youtube
すると四角錐kaefj と三角錐kefh に分かれる。 四角錐は台形aefj を底面として高さがak なので (26)×6÷2×2÷3=16 体積16cm 3 三角錐は efh が底面で kから面efghにおろした垂線の長さが高さである。 よって体積は6×6÷2×6÷3=36 よって3616=52 となる三角錐abcdが、 bcdを底面にして、机の上に置かれている。辺の長さをそれぞれ、 ab=1、ac= 、ad= 、bc= 、bd= 、cd=3 とする。このとき、三角錐abcdの体積を求めよ。 (答) 1/2 よおすけさんになりかわって解いてみた。図の四角すいの体積を求めなさい。 問題の見方 問題1と同様に, $$(底面積)×(高さ)×\frac{1}{3}=(体積)$$ で求めましょう。底面積はこの部分です。 高さは,図からこの部分だとわかります。 解答 底面積は一辺5cmの正方形の面積,高さは6cmになるので,
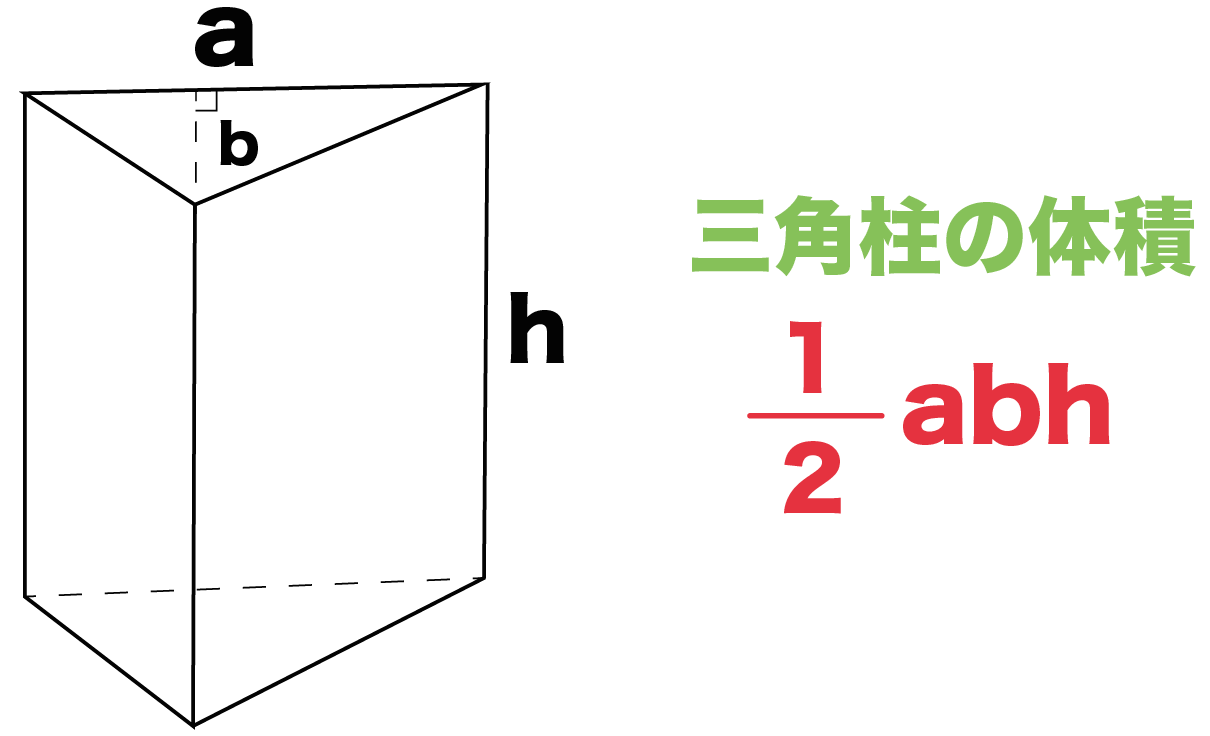


計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく



モデルの体積を計算する 試行錯誤
V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体今回は、体積の公式の求め方、覚え方と一覧、三角柱、円柱、三角錐の体積について説明します。体積の意味など下記も参考になります。 体積と重量の違いは?1分でわかる重量の計算、比重との違い、鉄の重量換算 三角錐の体積=3×4÷2×5÷3=10cm 3



計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
三角錐(さんかくすい、英 triangular pyramid, trigonal pyramid )や四面体(しめんたい、英 tetrahedron )とは、垂直断面に三角形を持つ錐体のことである。 辺6本、頂点4つからなる。 面の数は立体に於ける最小限界の4つであることから四面体とも呼ぶ。三角錐は、最小の頂点数で構成することが三角錐の体積の求め方の公式は?? こんにちは!この記事をかいているKenだよ。タルト最高。 三角錐の体積の求め方 には公式があるよ。 底面積をS、高さをhとすると、 三角錐の体積は、 1/3 Sh になるんだ。 つまり、 (底面積)×(高さ)÷ 3 ってわけだね。高校一年の数学Ⅰの三角錐の体積を求める問題です。 問題pa=pb=pc=4、ab=6、bc=4、ca=5である三角錐pabcの体積vを求めよ。 三角錐の高さの求め方。体積を求めるために、高さがわかりません>< わかっているのは各辺の長さと底面の一つのcosだけです。



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



高校数学 正四面体の高さと体積 練習編 映像授業のtry It トライイット
18年に京都府で行われた公立入試の前期問題問5の解説です。 問5は空間図形です。 空間図形では次元を下げれば平面なので、方針は1つで良いです。 また、この問題は見分けがつきにくいようで実は非常に簡単な問題なのでさっと18年に京都府で行われた公立入試の前期問題問5の解説です。 問5は空間図形です。 空間図形では次元を下げれば平面なので、方針は1つで良いです。 また、この問題は見分けがつきにくいようで実は非常に簡単な問題なのでさっと高校 入試(高校 (2)この三角錐を、\(3\) 点 \(p,q,r\) を通る平面で切断したとき、点 \(o\) を含む立体の体積は、もとの三角錐の体積の何倍か求めなさい。 高校入試数学の難問円・相似と三平方の定理の総合;



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



どうして1 3なの 錐の体積の公式の求め方 まなべーと
相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの三角錐(さんかくすい、triangular pyramid, trigonal pyramid)とは、垂直断面に三角形を持つ錐体のことである。 辺6本、頂点4つからなる。 さらに、面の数は立体に於ける最小限界の4つである。このことからまた、四面体(しめんたい、tetrahedron)とも呼ぶ。三角錐は、最小の頂点数で構成することが18年に京都府で行われた公立入試の前期問題問5の解説です。 問5は空間図形です。 空間図形では次元を下げれば平面なので、方針は1つで良いです。 また、この問題は見分けがつきにくいようで実は非常に簡単な問題なのでさっと



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



平成28年度 慶應義塾高等学校 数学 ますいしいのブログ
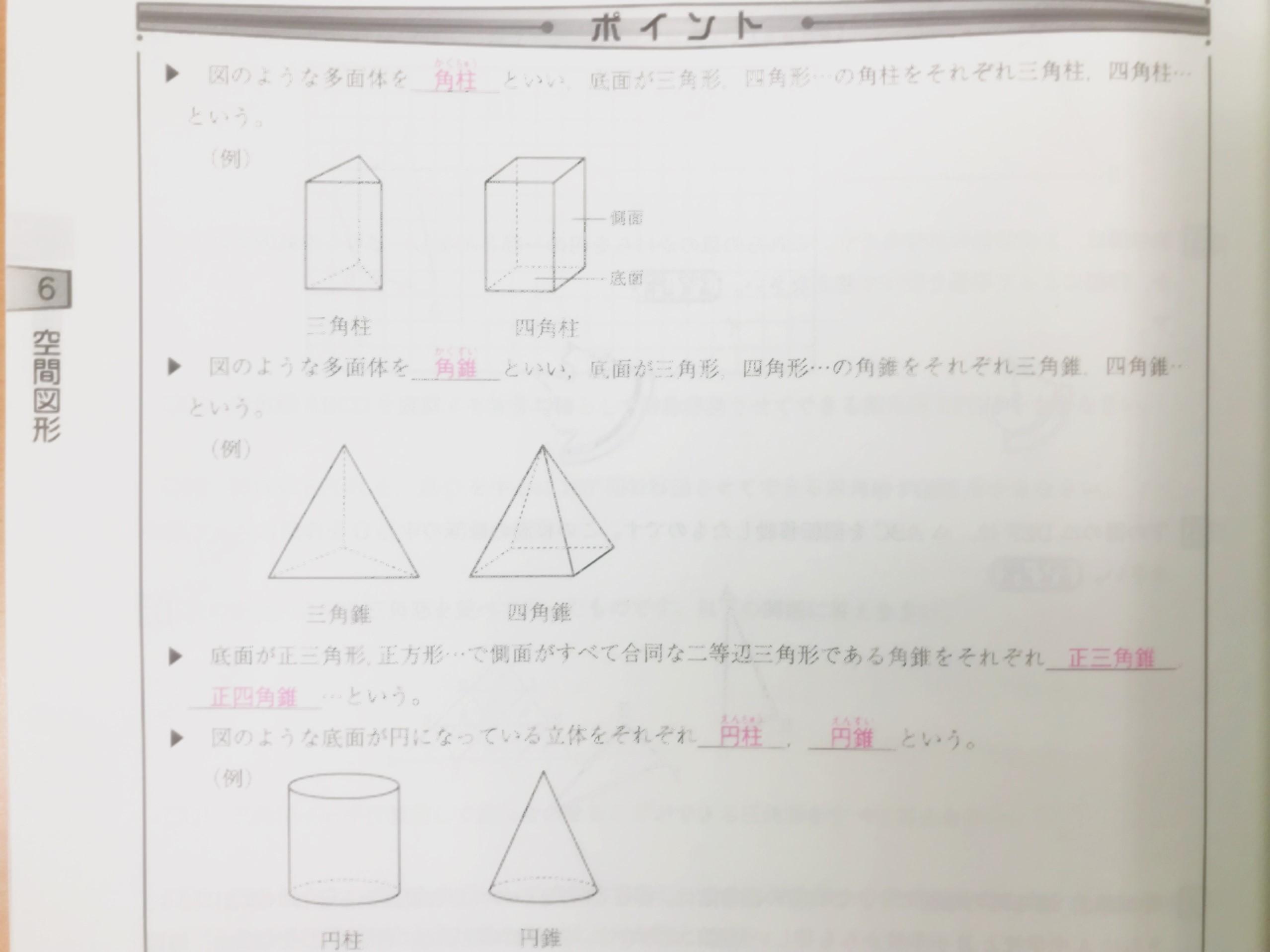


角柱 円柱 角錐 円錐の体積 滋賀県栗東市の個別塾 学習塾 ナビ個別指導学院 栗東校ブログ



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
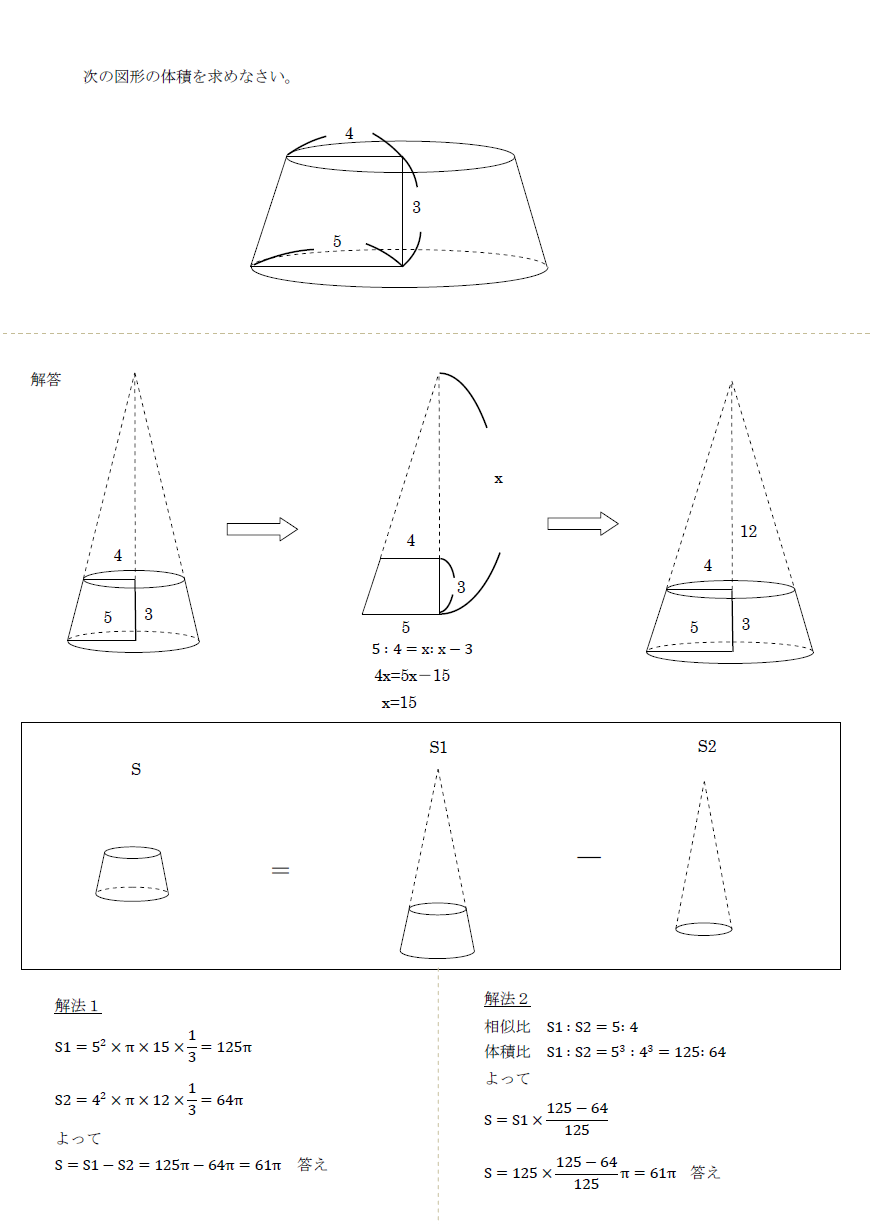


空間図形の体積 円錐台 の解法 中学 受験 定期試験 数学解き方集 裏技 解法



怜悧玲瓏 高校数学を天空から俯瞰する
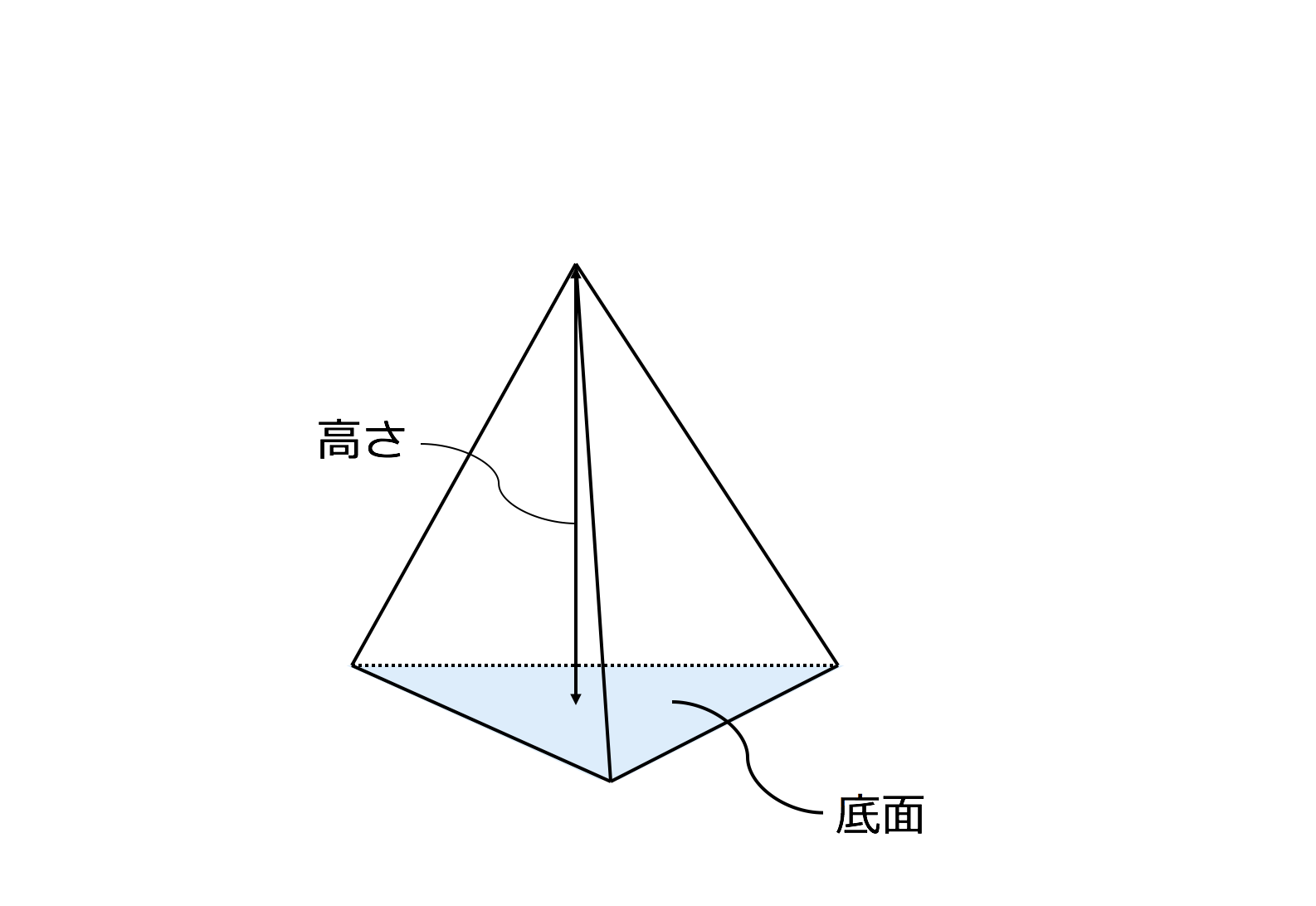


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ
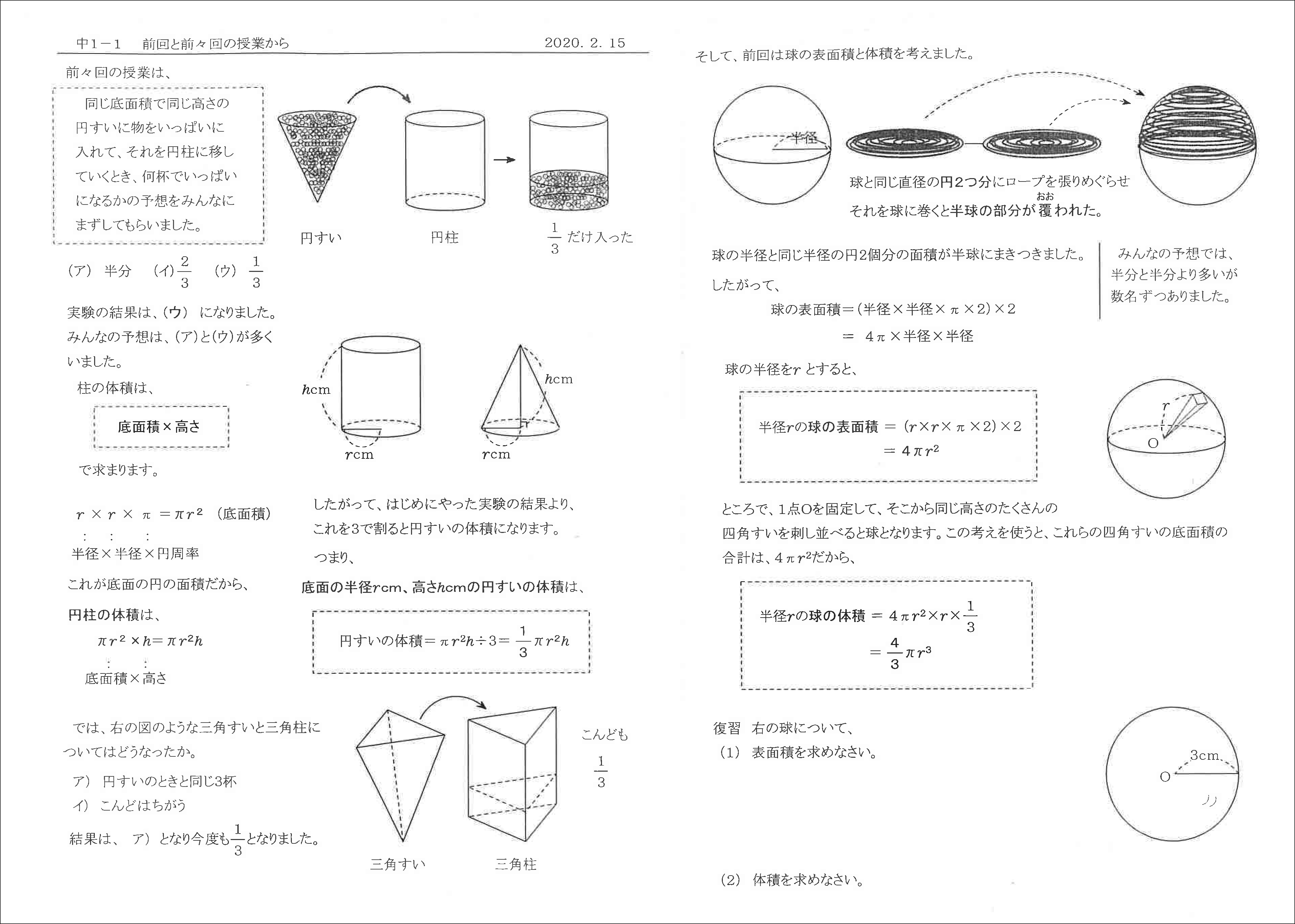


中1 立体の体積 東京女子学園中学校 高等学校
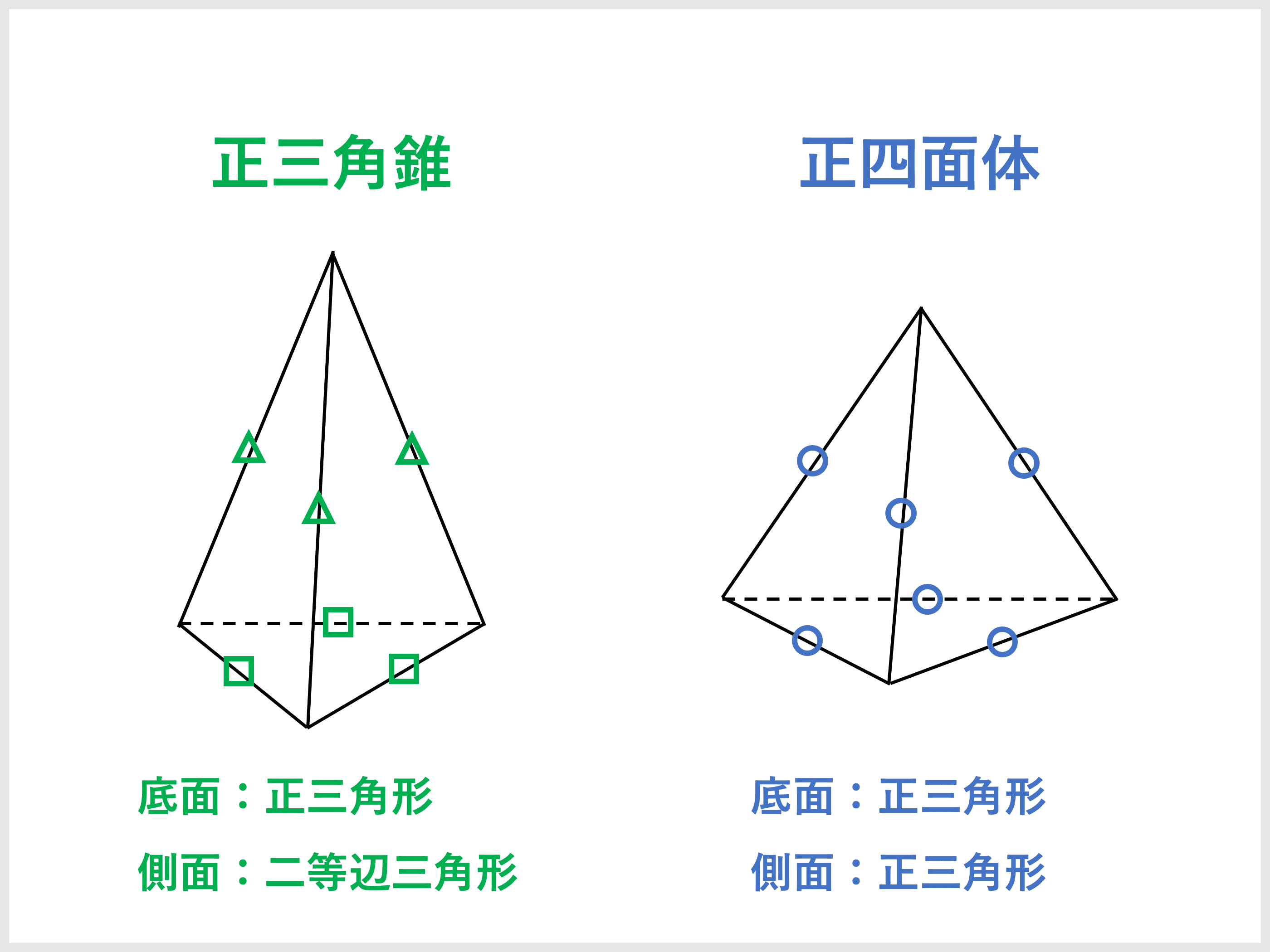


三角錐とは 体積 表面積の公式や求め方 受験辞典



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ



空間図形15 断頭三角柱の体積 Youtube



中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



相似な図形の問題です 中学数学に関する質問 勉強質問サイト
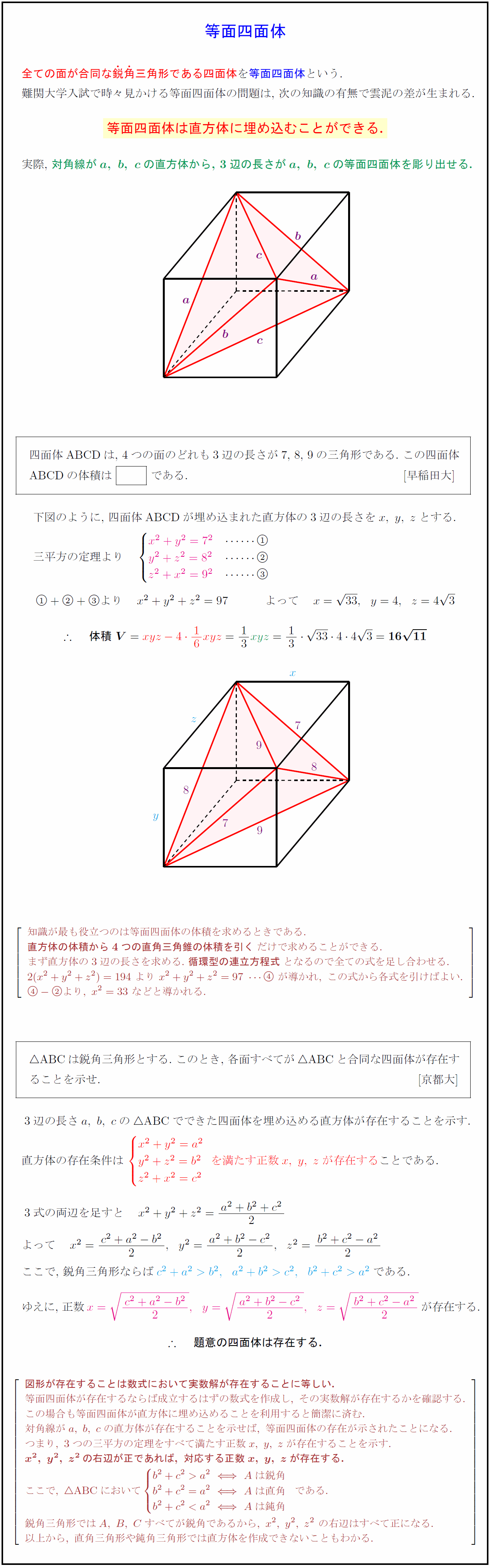


高校数学 等面四面体の体積と直方体への埋め込みと存在証明 受験の月



三角錐の体積に関するある私立中学校の入試問題 身勝手な主張
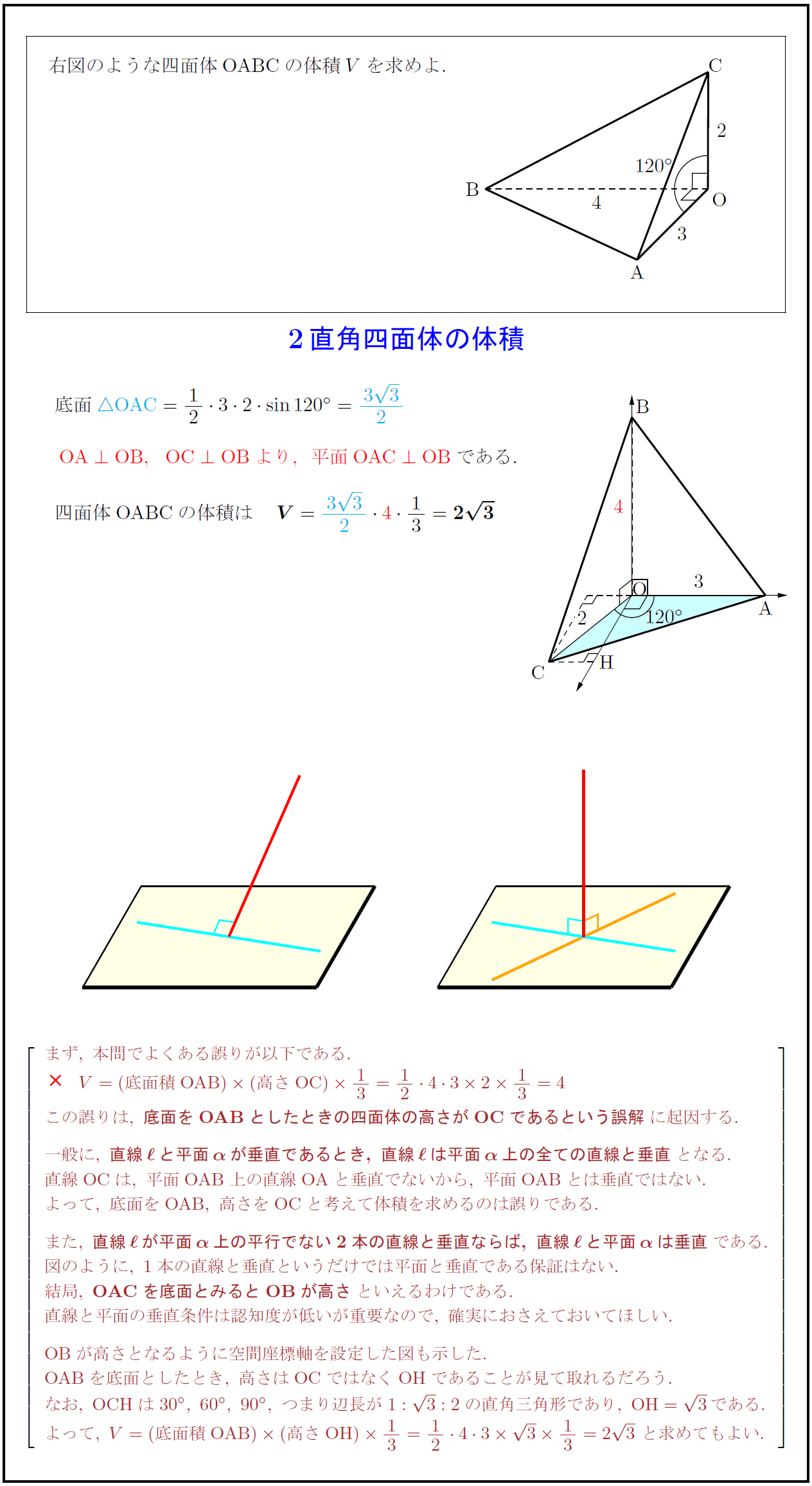


高校数学 2直角四面体の体積 直線と平面の垂直条件 受験の月
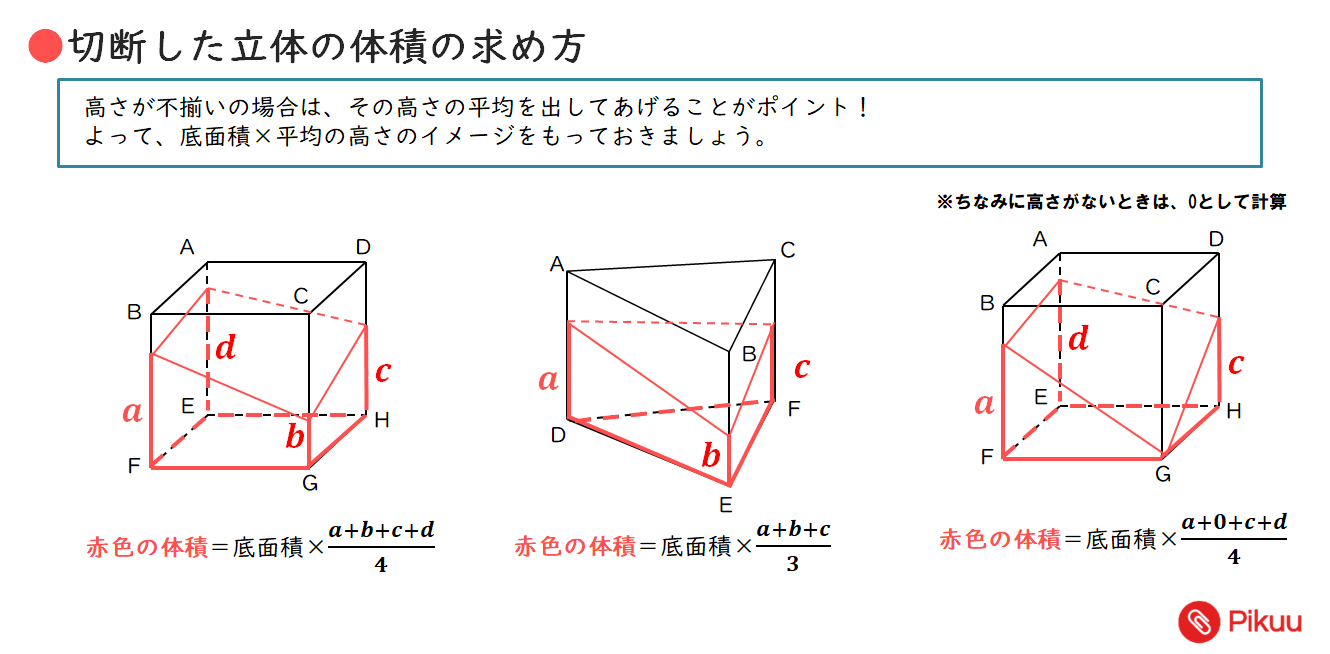


高校入試対策数学 知って得 中学数学の公式テクニック集 Pikuu



中1数学 13 6 角錐 円錐の体積 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ



三角錐とは 体積 表面積の公式や求め方 受験辞典



円錐の体積ってなんであの公式なの Webty Staff Blog
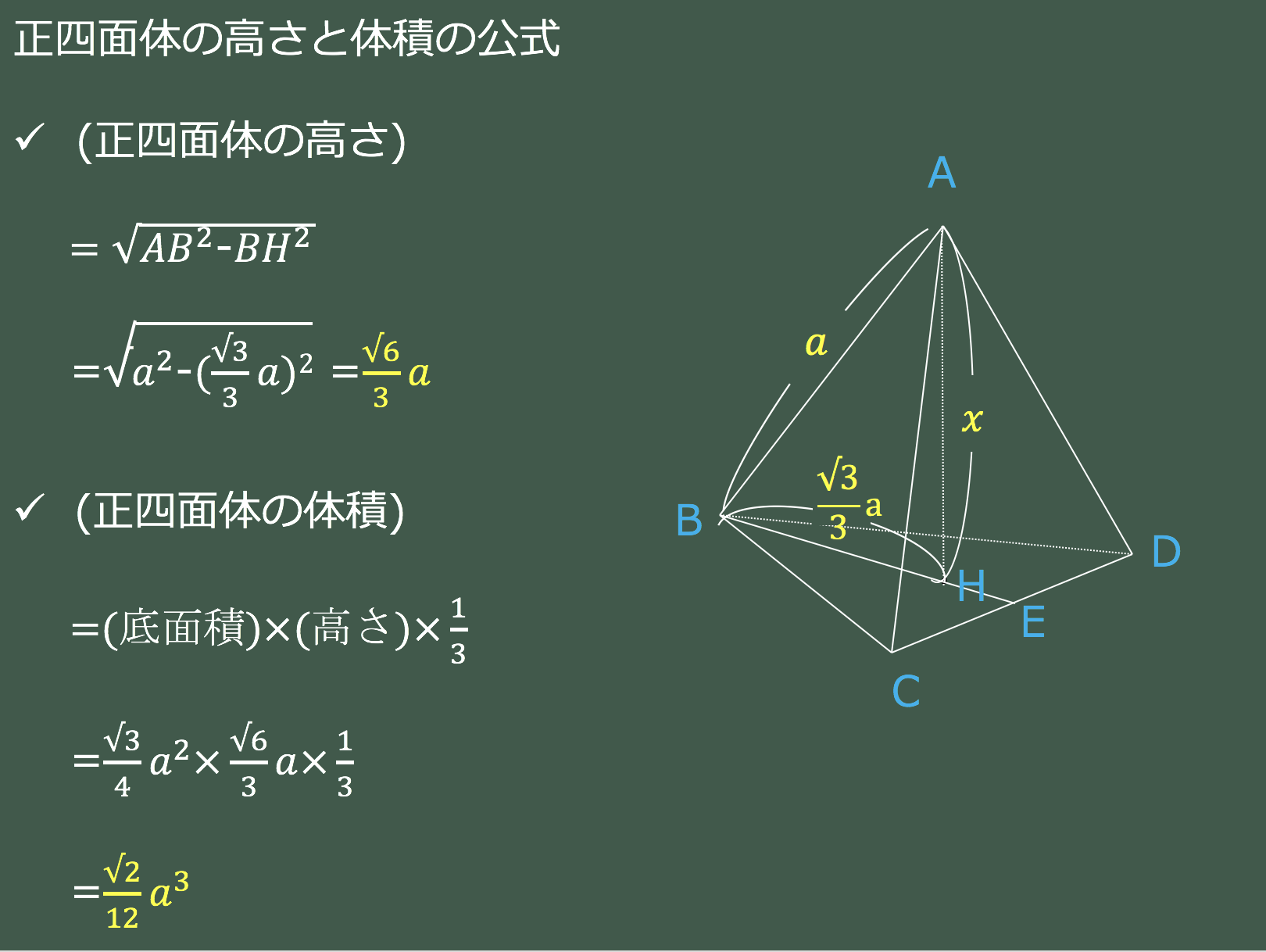


3分で分かる 正四面体の高さ 体積の求め方をわかりやすく 合格サプリ
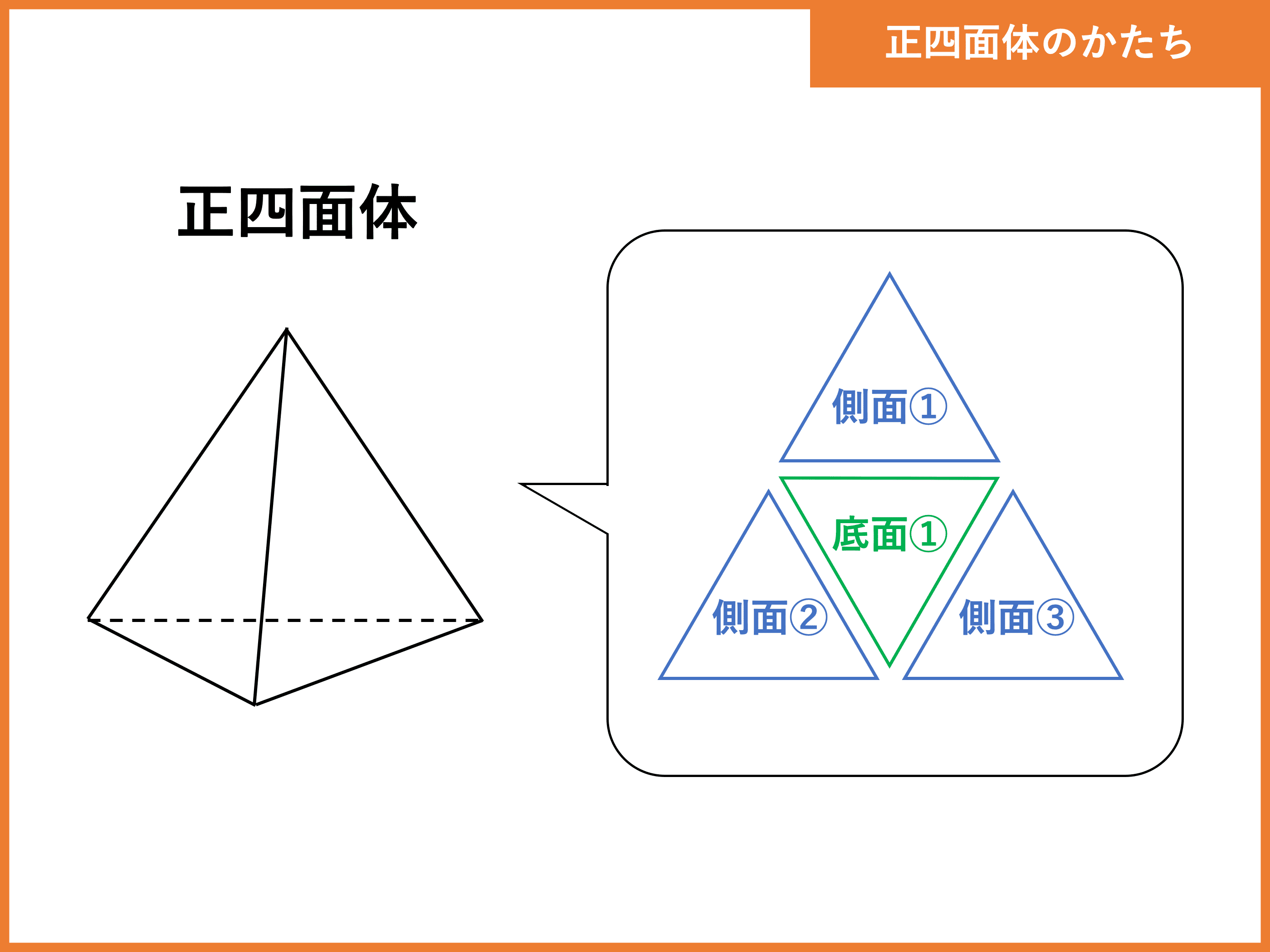


正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典



中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



Wd24n364jdi7im



体積比の問題です 中学数学に関する質問 勉強質問サイト



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく



中1数学 円すいの問題 練習編 映像授業のtry It トライイット



簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



この問題は 三角錐を2個タスのでしょうか 高校数学に関する質問 勉強質問サイト


Core Ac Uk Download Pdf Pdf



数学 中学数学に関する質問 勉強質問サイト



この三角錐の体積とその求め方を教えてください よろしくお願いします Clear
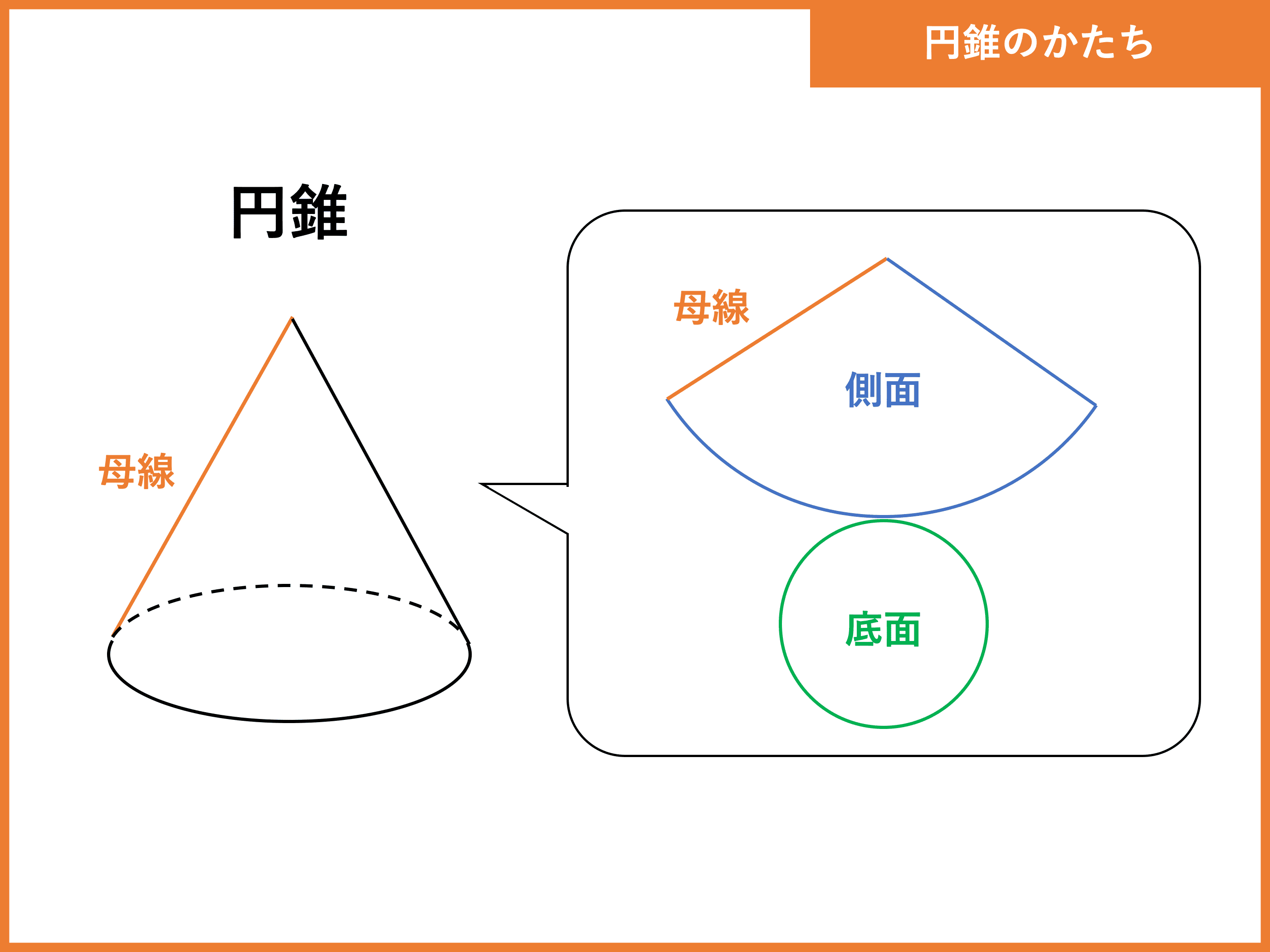


円錐とは 体積 表面積の公式や求め方 受験辞典



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
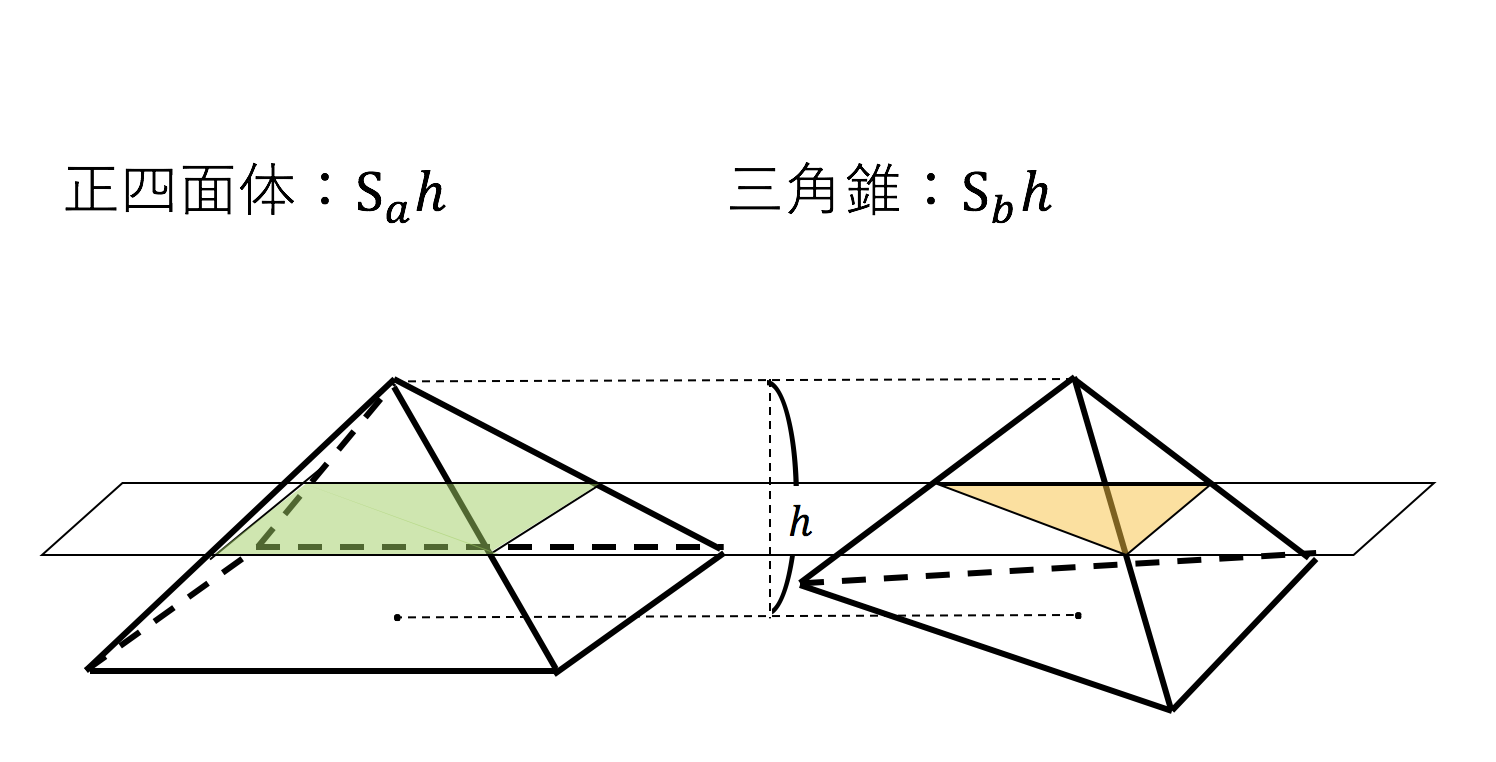


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ
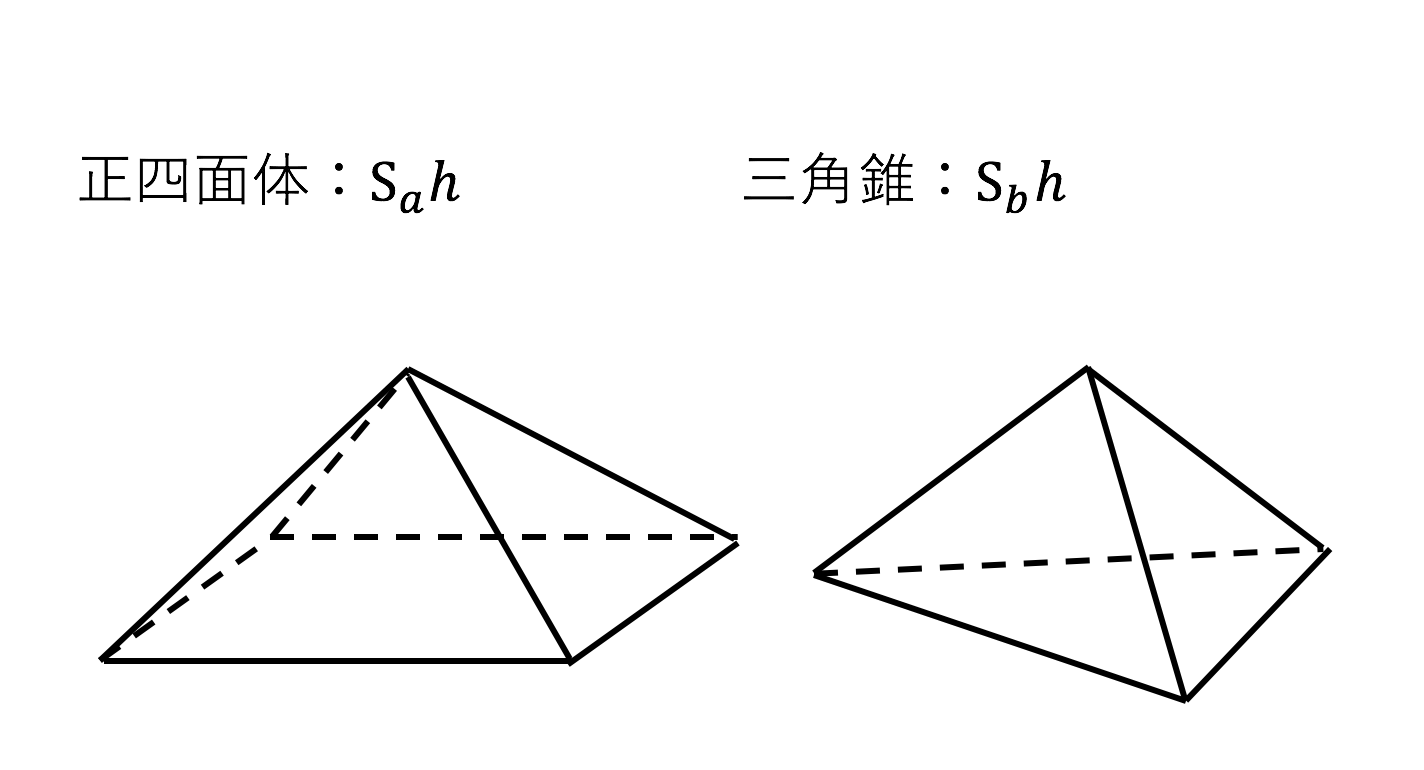


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



中学数学発展 空間図形の良難問とその解説 公立高校入試過去問より 定期テストや高校入試に レオンの中学数学探検所


三角錐とは 体積 表面積の公式や求め方 受験辞典


三角錐とは 体積 表面積の公式や求め方 受験辞典



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ



モデルの体積を計算する 試行錯誤



簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ



高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月



回転体 円錐の体積と表面積の求め方 現役塾講師のわかりやすい中学数学の解き方



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
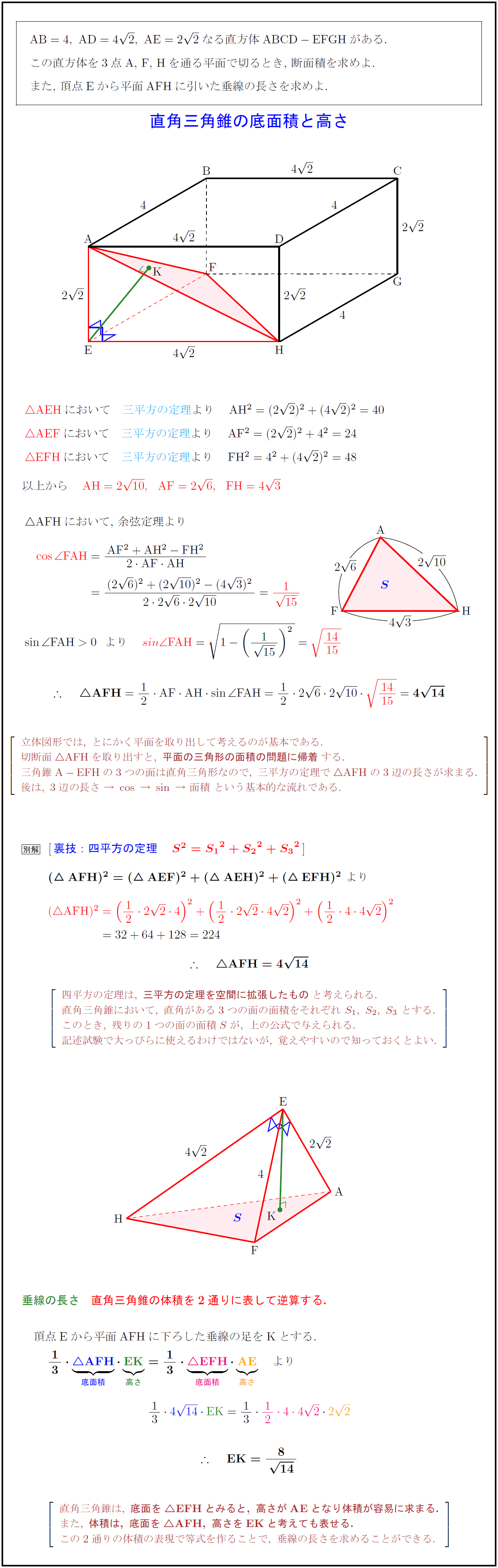


高校数学 直角三角錐 3直角四面体 の底面積と高さ 裏技 四平方の定理 受験の月



三角比 怜悧玲瓏 高校数学を天空から俯瞰する
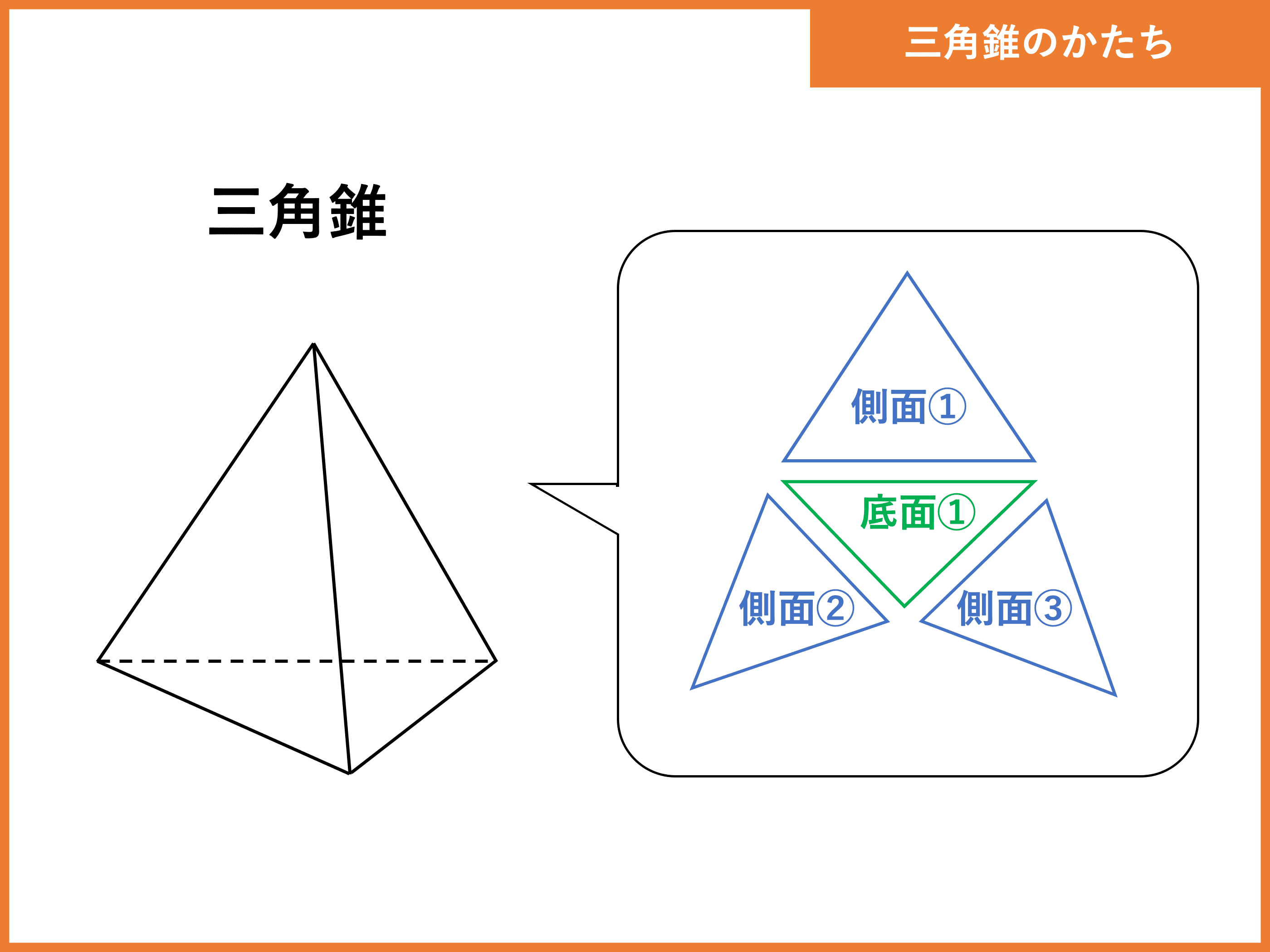


三角錐とは 体積 表面積の公式や求め方 受験辞典



円錐 問題 幼児 小学生 中学生の無料知育教材 無料学習教材プリント



高校数学 対称面をもつ四面体の体積 受験の月
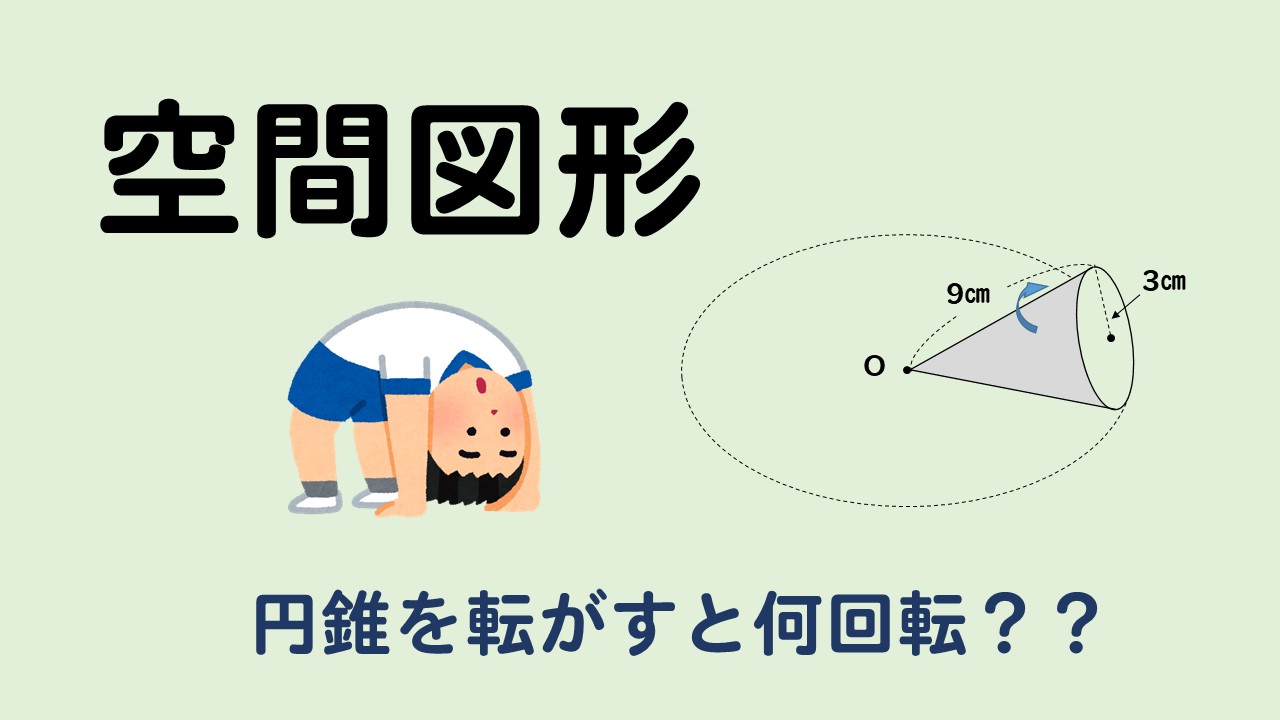


円錐を転がすと1周するのにどれくらい回転する 入試問題を解説 数スタ
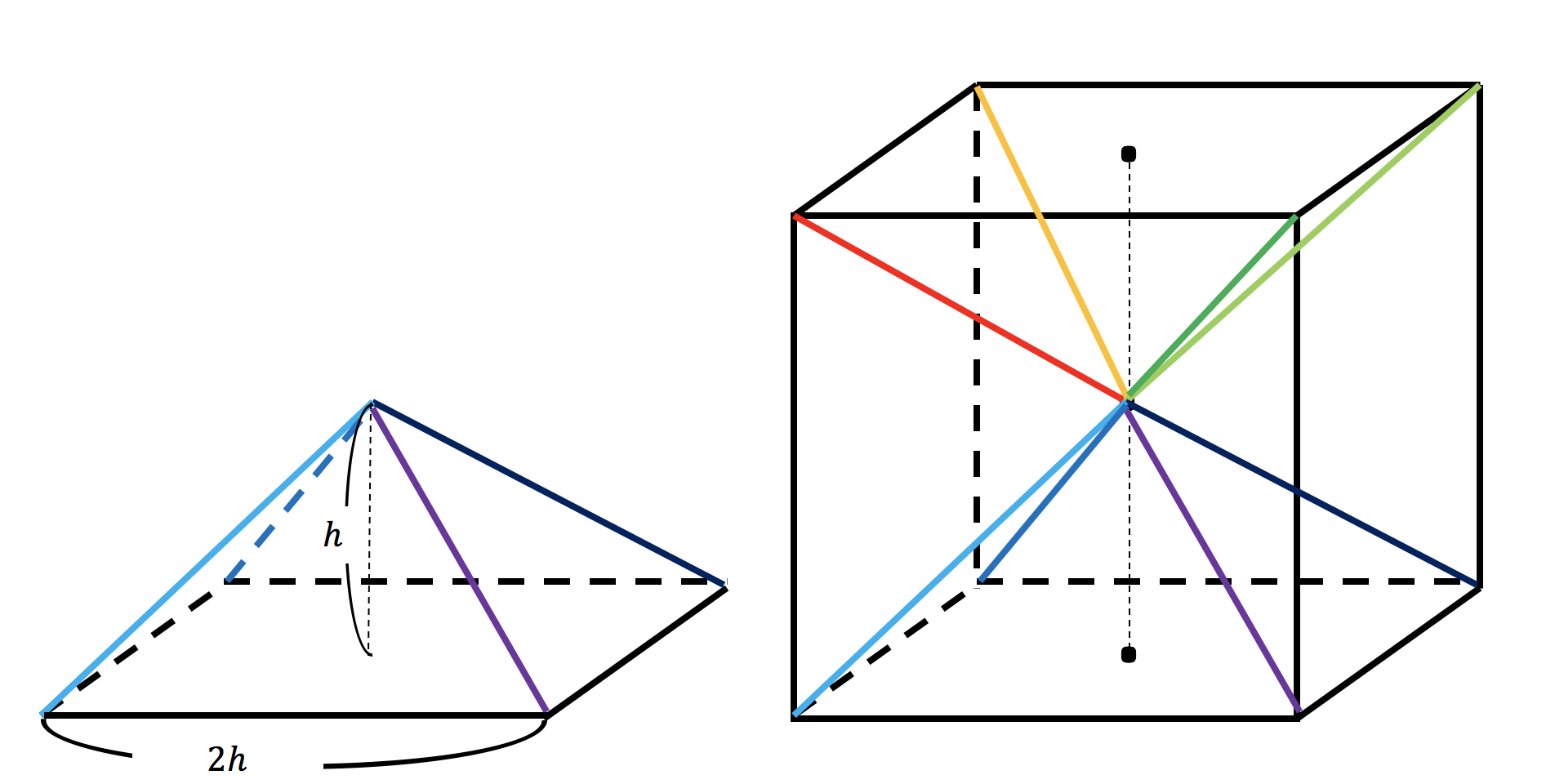


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



三角柱 台形 変な形の体積を求めよう 個別指導学院core コア 西川口の個別指導塾
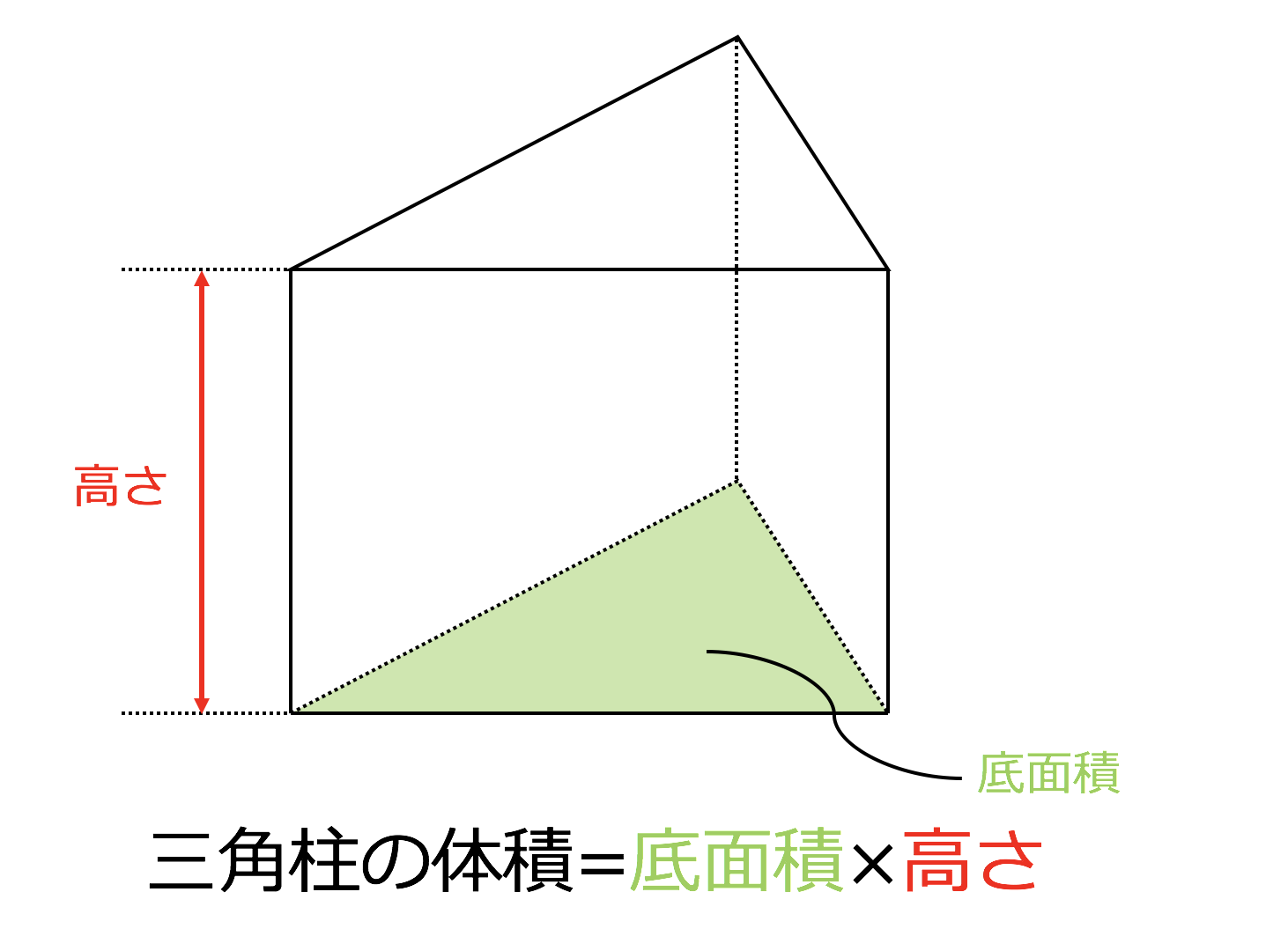


3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ
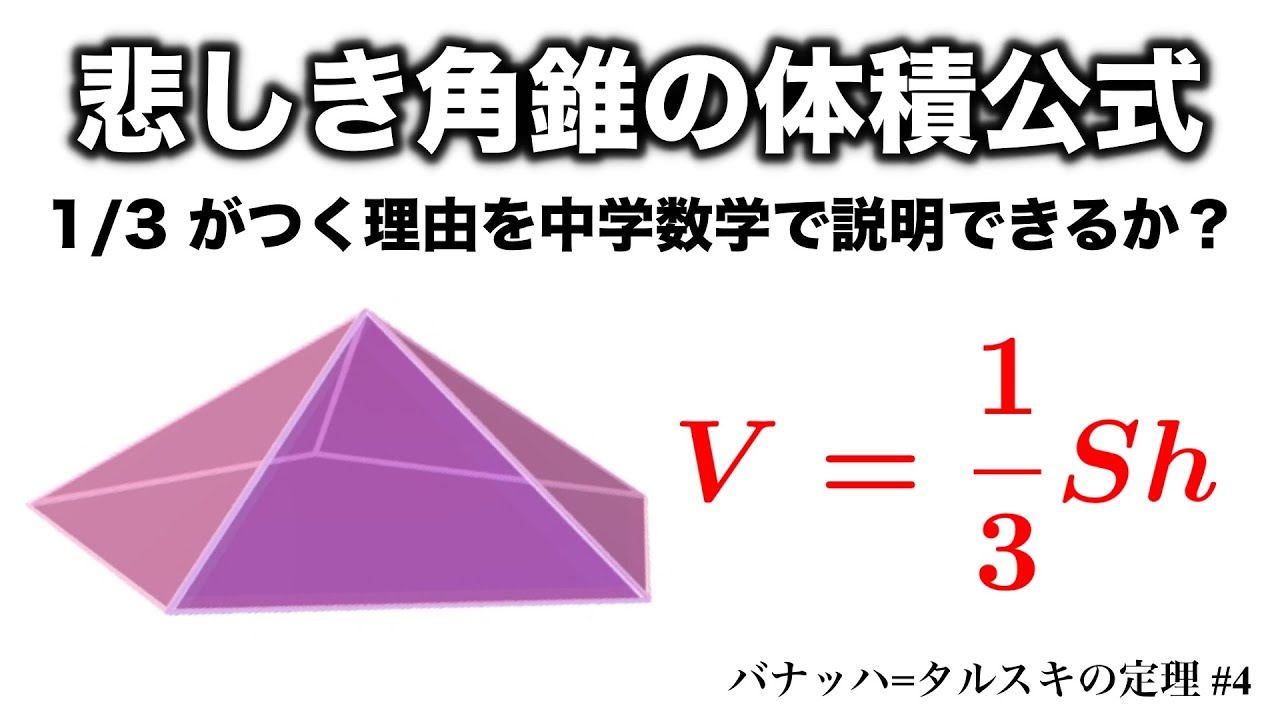


悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube



中学 数学 テクニック 三角錐の体積比 高校入試 高校受験 裏ワザ Youtube



嵯峨野こすもす数学入試問題解説 英語と数学を勉強法から教えます
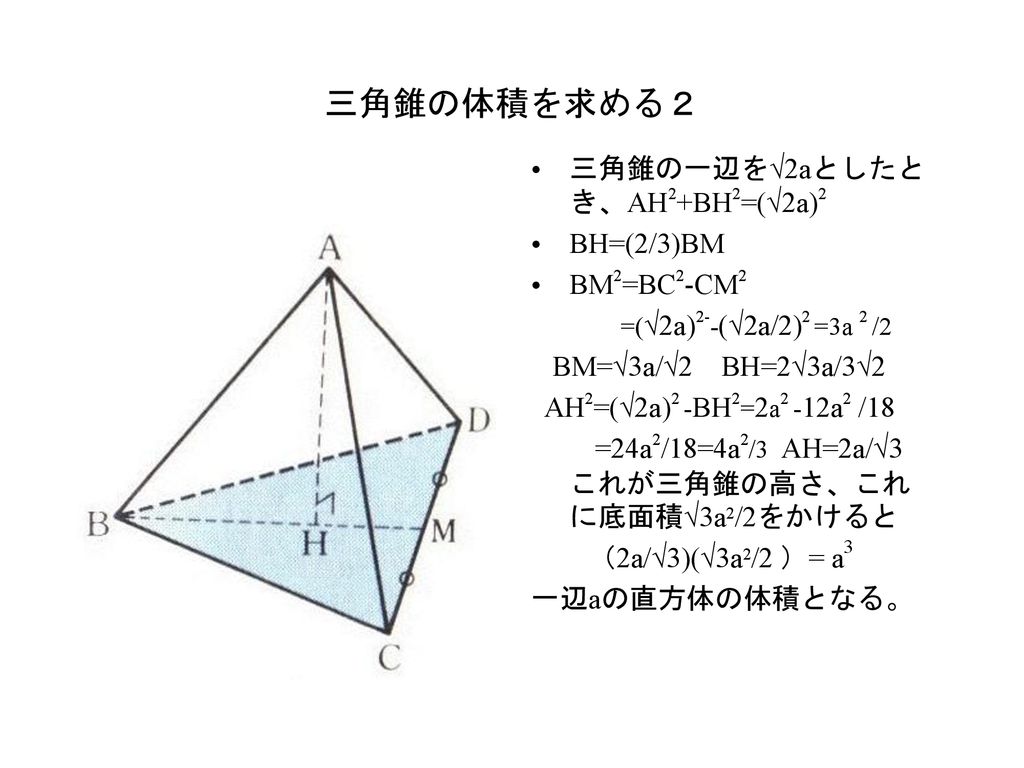


三角錐の体積 積分学まで待たねばならないか Ppt Download



空間図形14 円すい台の体積 Youtube



簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円錐の体積を求める Youtube



嵯峨野こすもす数学入試問題解説 英語と数学を勉強法から教えます
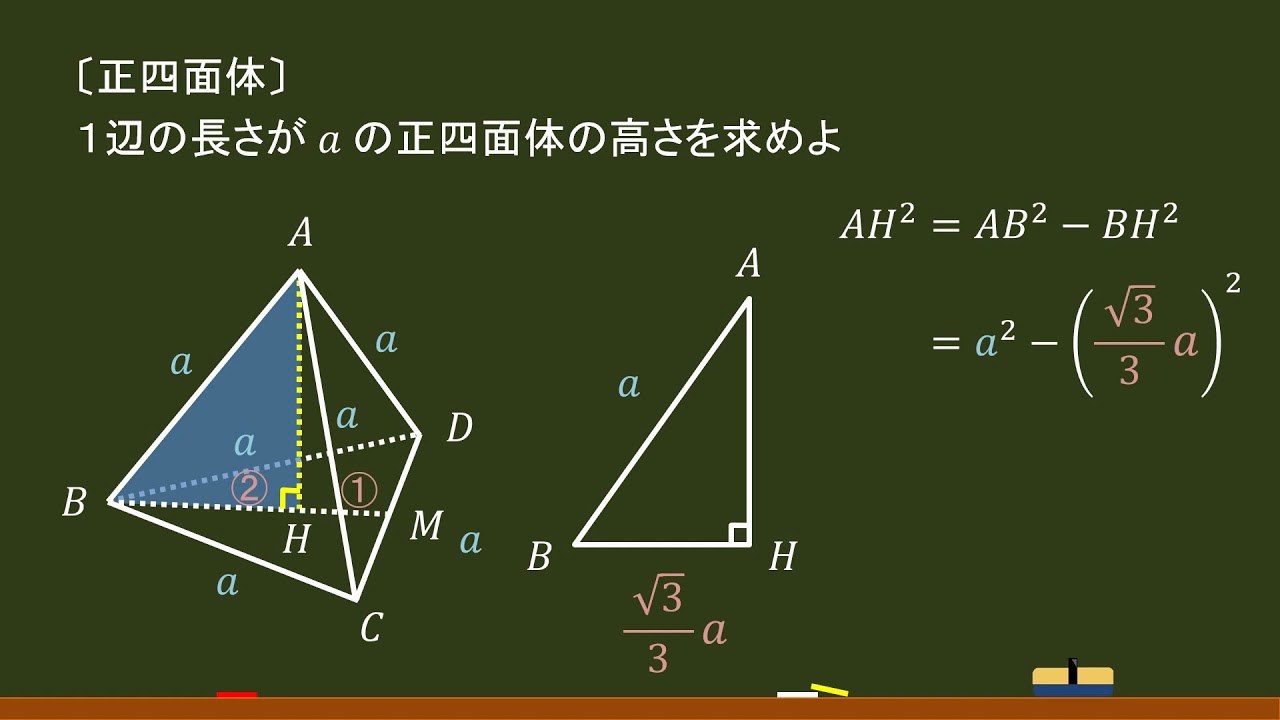


高校数学 正四面体 高さ 体積 オンライン無料塾 ターンナップ Youtube



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



展開図 立体組み立て ひもかけ 問題 神奈川県立 数学カフェjr



高校数学 立体 正四面体 直円錐 表面上の最短経路 受験の月



高校入試問題 空間図形 三角錐 体積から高さを求める Youtube



6辺の長さから四面体の体積を求める例題 怜悧玲瓏 高校数学を天空から俯瞰する


Core Ac Uk Download Pdf Pdf



โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clear



愛されし者 側 面積 求め 方 壁紙 配布


Core Ac Uk Download Pdf Pdf



年の最高 図形 の 面積 無料の印刷物
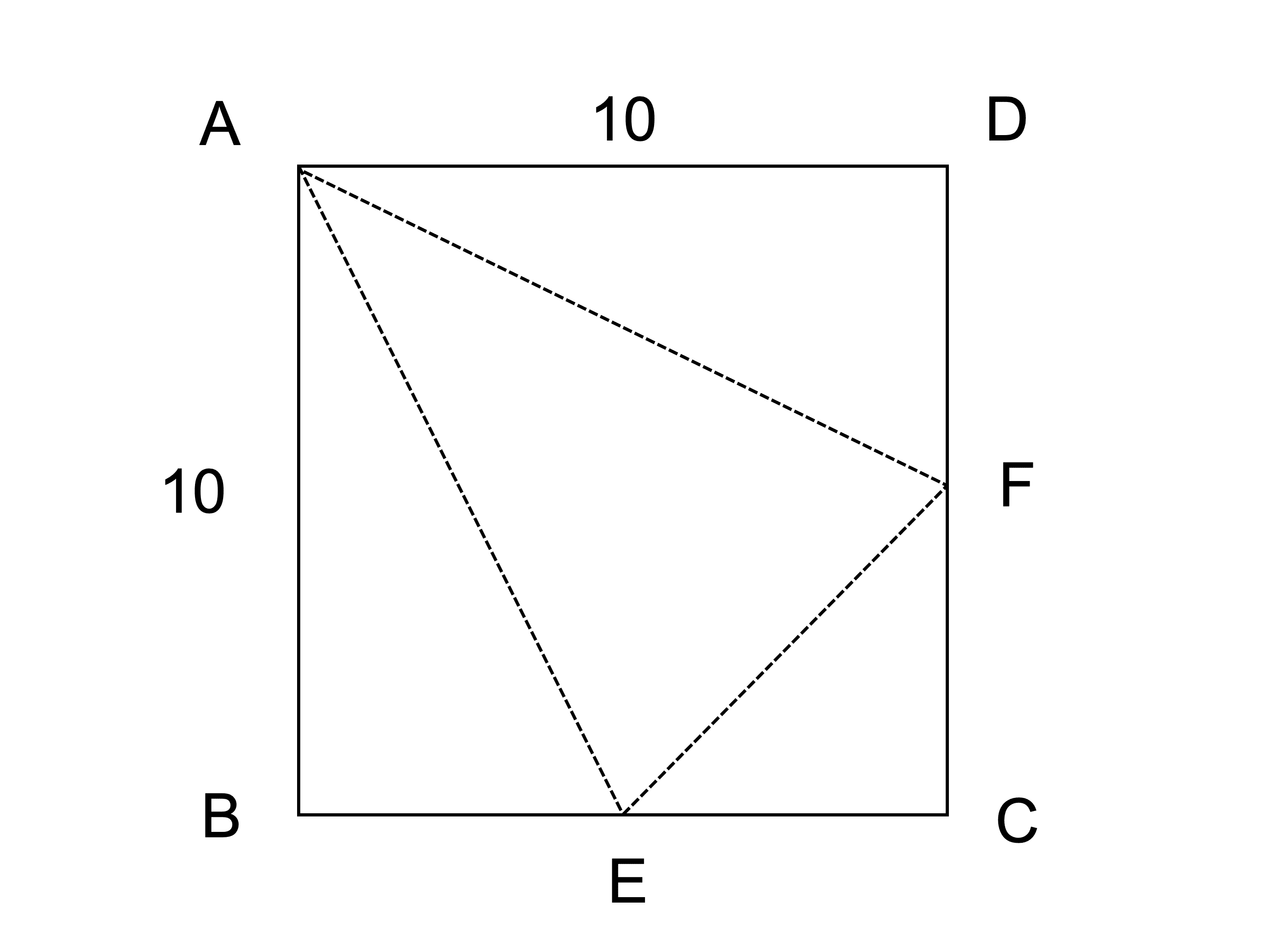


三角錐とは 体積 表面積の公式や求め方 受験辞典



数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear



数学カフェjr



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中3 三角形の相似 円錐の体積比 日本語版 Youtube



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ



展開図の良問難問 神奈川県 高校入試 数学 良問 難問



0 件のコメント:
コメントを投稿